Question
Show that the line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.
Solution
Given: A parallelogram ABCD in which M and N are the mid-points of a pair of its opposite sides AB and DC respectively.
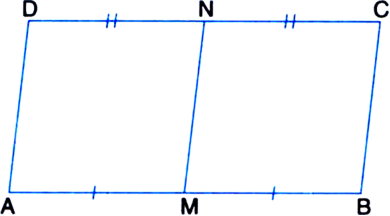
To Prove: ar(|| gm AMND) = ar(|| gm MBCN). Proof: ∵ ABCD is a || gm
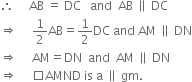

To Prove: ar(|| gm AMND) = ar(|| gm MBCN). Proof: ∵ ABCD is a || gm
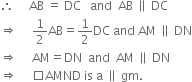
Similarly, we can prove that □MBCN is a parallelogram.
∵ || gm AMND and || gm MBCN are on equal bases AM and MB (∵ M is the mid-point of AB) and between the same parallels AB and DC.
∴ ar(|| gm AMND) = ar(|| gm MBCN).