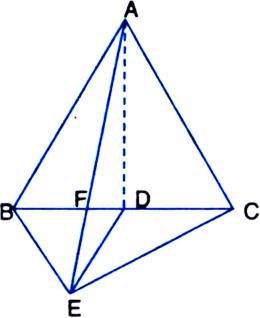
In figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
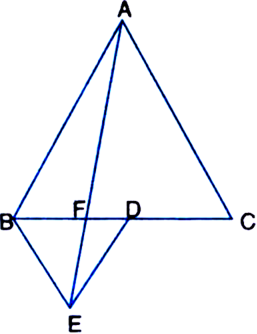
Given: ABC and BDE are two equilateral triangles such that D is the mid-point of BC. AE intersects BC at F.
Proof: ∵ ΔABC is an equilateral triangle. ∴ ∠ABC = ∠BCA = ∠CAB = 60° ...(1)
∵ ΔBDE is an equilateral triangle.
∴ ∠BDE = ∠DEB = ∠EBD = 60° ...(2) ∠ABE + ∠BED
= ∠ABD + ∠EBD + ∠BED = 60°+ 60°+ 60°= 180°
∴ AB || DE ...(3)
∵ Sum of consecutive interior angles on
the same side of a transversal is 180° ∠EBA + ∠BAC
= ∠EBD + ∠DBA + ∠BAC = 60° + 60° + 60° = 180°
∴ AC || BE ...(4)
∵ Sum of consecutive interior angles on the same side of the transversal is 180°
∵ ΔCBA and ΔCEA are on the same base AC and between the same parallels.
∴ ar(ΔCBA) = ar(ΔCEA)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area ⇒ ar(ΔABC) = ar(ΔCDA) + ar(ΔCED) + ar(ΔADE) ...(5)
In ΔABC,
∵ AD is a median.
∵ A median of a triangle divides it into two triangles of equal area
In ΔEBC,
∵ ED is a median.
∵ A median of a triangle divides it into two triangles of equal area ∵ ΔDEA and ΔDBE are on the same base DE and between the same parallels AB and DE.
∴ ar(ΔDEA) = ar(ΔDBE) ...(8)
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in area
Using (6), (7) and (8), (5) gives
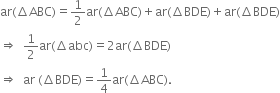
(ii) ∵ ΔBAE and ΔBCE are on the same base BE and between the same parallels BE and AC.
∴ ar(ΔBAE) = ar(ΔBCE)
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in
area
⇒ ar(ΔBAE) = 2 ar(ΔBDE)
| From (7)
(iii) 2 ar(ΔBEC) = 2.2 ar(ΔBDE)
| From (7)
= 4 ar(ΔBDE) = ar(ΔABC).
| Form (i)
(iv) ∵ ΔEBO and ΔEAD are on the same base ED and between the same parallels AB and DE.
∴ ar(ΔEBD) = ar(ΔEAD).
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in area ⇒ ar(ΔEBD) – ar(ΔEFD)
= ar(ΔEAD) – ar(ΔEFD)
| Subtracting the same areas from both sides ⇒ ar(ΔBFE) = ar(ΔAFD).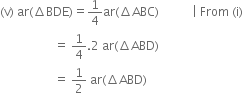
∵ Bases of ΔBDE and ΔABD are the same.
ar (ΔBEF) = ar(ΔAFD) ...(10) | From (iv)
Altuitude of 
Altitude of 
| From (9)
Altitude of 
Altitude of 
From (10) and (11),
BF = 2FD ...(12)
In ΔBFE and ΔFED,
∵ BF = 2FD and, alt (ΔBFE) = alt (ΔFED) ar(ΔBFE) = 2 ar(ΔFED).
(vi) Let the altitude of ΔABD be h.
Then, altitude of 
Now, 
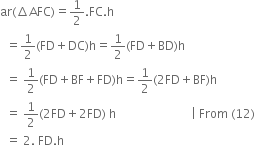
From (13) and (14), we obtain,
