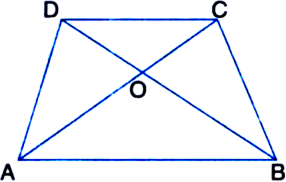
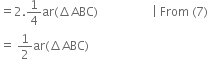D, E and F are respectively the midpoints of the sides BC, CA and AB of a ΔABC. Show that:

(i) BDEF is a parallelogram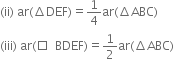

Given: D, E and F are respectively the midpoints of the sides BC, CA and AB of a ΔABC.

To Prove: (i) □BDEF is a parallelogram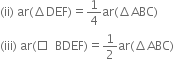

Proof: (i) In ΔABC,
∵    F is the mid-point of side AB and
E is the mid-point of side AC.
∴ EF || BC
∵ In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side.

⇒    EF || BD    ...(1)

Similarly, ED || BF    ...(2)
In view of (1) and (2),
□ BDEF is a parallelogram.
∵    A quadrilateral is a parallelogram
if its opposite sides are parallel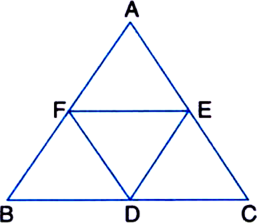

(ii) As in (i), we can prove that
□AFDE and □FDCE are parallelograms.
∵    FD is a diagonal of || gm BDEF.
ar(ΔFBD) = ar(ΔDEF) ...(3) Similarly, ar(ΔDEF) = ar(ΔFAE) ...(4) and,    ar(ΔDEF) = ar(ΔDCE) ...(5)
From (3), (4) and (5), we have ar(ΔFBD) = ar(ΔDEF)
= ar(ΔFAE) = ar(ΔDCE) ...(6)
∵    ΔABC is divided into four non-overlapping triangles ΔFBD, ΔDEF, ΔFAE and ΔDCE.
∴ ar(ΔABC) = ar(ΔFBD) + ar(ΔDEF) + ar(ΔFAE) + ar(ΔDCE) = 4 ar(ΔDEF) | From (6)
⇒ ar(ΔDEF) = 1/2 ar(ΔABC).    ...(7)
4
(iii) ar(□BDEF)
= ar(ΔFBD) + ar(ΔDEF)
= ar(ΔDEF) + ar(ΔDEF)
| From (3)
= 2 ar(ΔDEF)