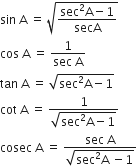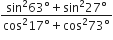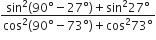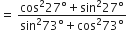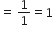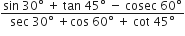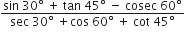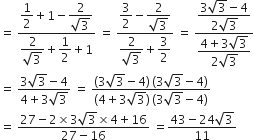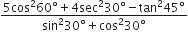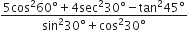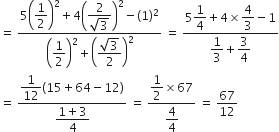गणित Chapter 8 त्रिकोणमिति का परिचय
Sponsor Area
NCERT Solution For Class 10 गणित गणित
ΔABC में, जिसका कोण B समकोण है, AB = 24 cm और BC = 7 cm है। निम्नलिखित का मान ज्ञात कीजिए:
(i) sin A cos A,
(ii) sin C, cos C.
हमे प्राप्त हैं, AB = 24 cm
BC = 7cm, पाइथागोरस प्रमेय के प्रयोग से,
AC2 = AB2 + BC2
= (24 cm)2+ (7 cm)2
= 576 cm2 + 49 cm2
= 625 cm2
So, AC = 25 cm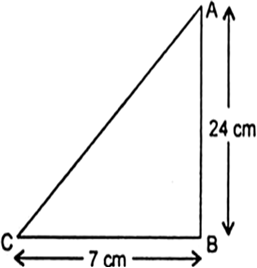
अब,
(i) 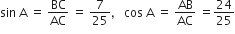
(ii) 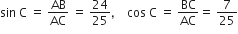
सलंग्न आकृति में tan p - cot R का मान ज्ञात कीजिए।
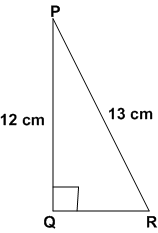
मान लीजिए:
PQ = 12K
तथा
PR = 13K
पाइथागोरस प्रमेय के प्रयोग से:
PR2 = PQ2 + QR2
⇒(13K)2 = (12K)2 + QR2
⇒169K2 = 144K2 + QR2
⇒QR2 = 169K2 - 144K2
⇒ QR2 = 25K2
∴ QR = 5K
अब, 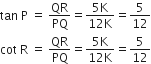
अत: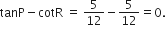
यदि 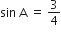 तो cosA तथा tanA का मान परिकलित कीजिए।
तो cosA तथा tanA का मान परिकलित कीजिए।
 माना कि ABC एक समकोण त्रिभुज है जिसमें
माना कि ABC एक समकोण त्रिभुज है जिसमें 
हम जानते हैं:
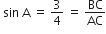
Let BC = 3K, AC = 4K
यहाँ k एक घनात्मक संख्या हैं।
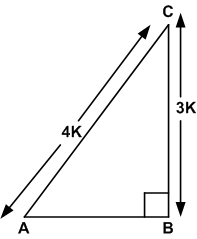
पाइथागोरस प्रमेय के प्रयोग से:






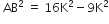


अब,
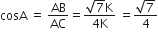
और

यदि 15cot A = 8 हो तो sinA और secA का मान ज्ञात कीजिए।
 माना कि एक समकोण त्रिभुज है जिसमें
माना कि एक समकोण त्रिभुज है जिसमें 
हमें दिया गया हैं:
15 cot A = 8

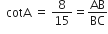
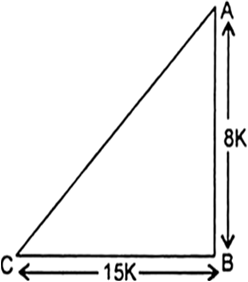
माना
AB = 8K, BC = 15K
पाइथागोरस प्रमेय के प्रयोग से:
AC2 = AB2 + BC2 = (8K)2 + (15K)2
= 64K2 + 225K2
= 289K2
अत;
AC = 17K
अब,
AC = 17K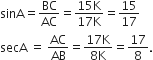
यदि 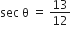 हो तो अन्य त्रिकोणमितीय अनुपात परिकलित कीजिए।
हो तो अन्य त्रिकोणमितीय अनुपात परिकलित कीजिए।
 एक समकोण त्रिभुज है जिसमें
एक समकोण त्रिभुज है जिसमें 
हम जानते हैं:
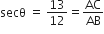
माना कि AB = 12 K, AC = 13K
यहाँ K एक घनात्मक संख्या हैं।
पाइथागोरस प्रमेय के प्रयोग से:
AC2 = AB2 + BC2
⇒(13K)2 = (12K)2 + BC2
⇒169K2 = 144K2 + BC2
⇒BC2 = 169K2-144K2
BC2 = 25K2 BC = 5K
BC = 5K
अब,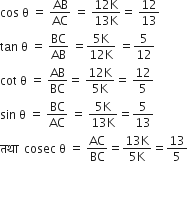
यदि  न्यून कोण हैं। जहां cosA = cosB तो दिखाइए कि
न्यून कोण हैं। जहां cosA = cosB तो दिखाइए कि 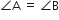 .
.
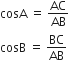
अत:
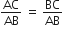
अर्थात् AC = BC
अत:
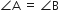

समान भुजाओं के सम्मुख कोण समान होते हैं।
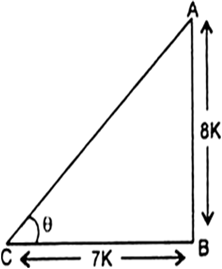
यदि cot θ =  तो
तो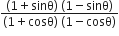
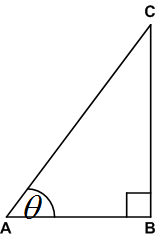
 एक समकोण त्रिभुज है, जिसमें
एक समकोण त्रिभुज है, जिसमें  .
.यहाँ,
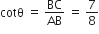
BC = 7K
माना BC = 7K
AB = 8K
पाइथागोरस प्रमेय के प्रयोग से:
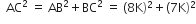
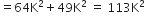


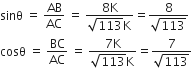
अब,
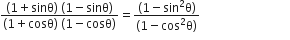
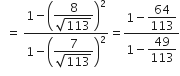
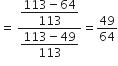
यदि 3 cot A = 4, तो जाँच कीजिए कि
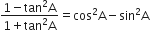 है या नहीं।
है या नहीं।
 एक समकोण त्रिभुज है जिसमें
एक समकोण त्रिभुज है जिसमें  .
.3 cot A = 4

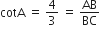
माना लीजिए, AB = 4K और BC = 3K
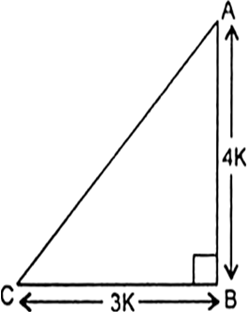
पाइथागोरस प्रमेय के प्रयोग से:
AC2 = AB2 + BC2
= (4K)2 + (3K)2
= 16K2 + 9K2 = 25K2
अत: AC = 5K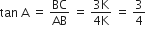
अब, 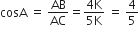
और 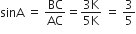
L.H.S. = 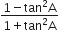
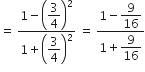
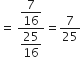
अब,
R.H.S. = 
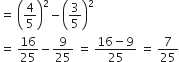
अत: L.H.S. = R.H.S.
अथवा 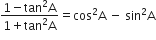
त्रिभुज ABC में, जिसका कोण B समकोण है, यदि 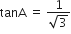 तो निम्नलिखित के मान ज्ञात कीजिए:
तो निम्नलिखित के मान ज्ञात कीजिए:
(i) sin A cos C + cos A sin C
(ii) cos A cos C - sin A sin C
हमें प्राप्त है: 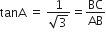
मान लीजिए: 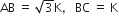
पाइथागोरस प्रमेय के प्रयोग से: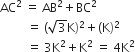
AC = 2K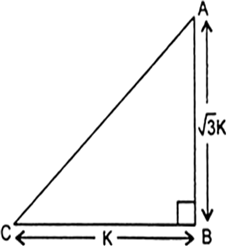
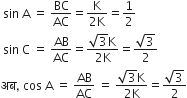
और, 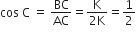
अब,
(i) sin A cos C + cos A sin C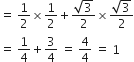
(ii) cos A. cos C - sin A. sin C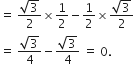
ΔPQR में, जिसका कोण Q समकोण है, PR + QR =25 cm तथा PQ = 5 cm है। sinP, cosP और tanP के मान ज्ञात कीजिए।
हमें प्राप्त है ,
PR + QR = 25 cm ..(i)
माना कि PR = x cm
QR = (25 - x) cm.
पाइथागोरस प्रमेय के प्रयोग से:
PR2 = PQ2 + RQ2
⇒ x2 = (52) + (25 - x)2
x2 = 25 + 625 + x2 - 50x
⇒ 50x = 650
⇒ x = 13 cm
अब,
PR = x = 13 cm, QR = (25 - x) = 12 cm
और PQ = 5 cm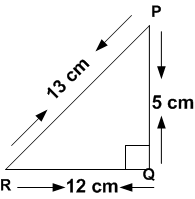
अब,
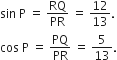
और 
बताइए कि निम्नलिखित कथन सत्य हैं या असत्य। कारण सहित अपने उत्तर की पुष्टि कीजिए।
-
tan A का मान सदैव 1 से कम होता है।
-
कोण A के किसी मान के लिए
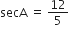
-
cos A, कोण A के cosecant के लिए प्रयुक्त एक संक्षिप्त रूप है।
-
cot A, cot तथा A का गुणनफल होता है।
-
cot A, cot तथा A का गुणनफल होता है।
(i) असत्य (क्योंकि 
 )
)
(ii) सत्य (क्योंकि विकर्ण, अन्य भुजा से बड़ा होता है।)
(iii) असत्य, (cosA कोण A से cosine के लिए प्रयुक्त एक संक्षिप्त रूप है।)
(iv) असत्य, (यह A का cotangent होता है।)
(v) असत्य (विकर्ण, अन्य भुजा से बड़ा होता है।)
निम्न के मान निकालिए:
sin 60° cos 30° + sin 30° cos 60°
=
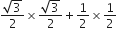
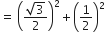
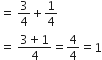 .
.
सही विकल्प चुनिए और अपने विकल्प का औचित्य दीजिए:
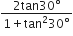
-
sin 60°
-
cos 60°
-
tan 60°
-
sin 30°
sin 60°
cos 60°
tan 60°
sin 30°
A.
sin 60°
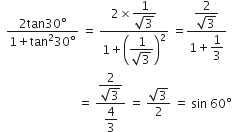
सही विकल्प चुनिए और अपने विकल्प का औचित्य दीजिए:
sin 2A = 2 sinA तब सत्य होता हैं, जबकि A बराबर है।
-
0°
-
30°
-
45°
-
60°
A.
0°
यदि, A = 0
तब, L.H.S. = sin 2A = sin 2(0)
= sin 0° = 0
R.H.S. = 2 sin A = 2 sin 0°
= 2 x 0 = 0
Sponsor Area
यदि 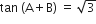 और
और 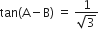 ;
;  तो A और B का मान ज्ञात कीजिए।
तो A और B का मान ज्ञात कीजिए।
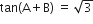
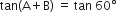
⇒ A + B = 60° ...(i)
और
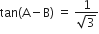
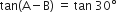
⇒ A - B = 30° ...(ii)
समीकरण (i) तथा (ii) को हल करने पर हमें प्राप्त होता हैं:
A = 45° and B = 15°.
बताइये कि निम्नलिखित में से कौन-कौन सत्य हैं या असत्य हैं। कारण सहित अपने उत्तर की पुष्टि कीजिए।
-
sin (A + B) = sinA + sinB
-
 में वृद्धि होने के साथ
में वृद्धि होने के साथ  के मान में भी वृद्धि होती है।
के मान में भी वृद्धि होती है।
-
θ में वृद्धि होने के साथ-साथ cosθ के मान में भी वृद्धि होती है।
-
θ के सभी मानों पर sin θ = cos θ
-
θ के सभी मानों पर sin θ = cos θ
sin (A + B) = sinA + sinB
 में वृद्धि होने के साथ
में वृद्धि होने के साथ  के मान में भी वृद्धि होती है।
के मान में भी वृद्धि होती है।
θ में वृद्धि होने के साथ-साथ cosθ के मान में भी वृद्धि होती है।
θ के सभी मानों पर sin θ = cos θ
θ के सभी मानों पर sin θ = cos θ

(ii) सत्य, क्योंकि
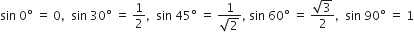
(iii) असत्य, क्योंकि
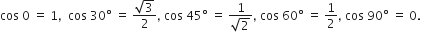
(iv) असत्य क्योंकि

(v) सत्य क्योंकि
 ।
।दिखाइए कि:
tan 48° tan 23° tan 42° tan 67° = 1.
L.H.S
= tan 48° . tan 23°. tan 42° . tan 67°
= tan 48° . tan 42° . tan 23° . tan 67°
= tan (90° - 42°). tan 42°. tan (90° - 67°). tan 67°
= cot 42° . tan 42° . cot 67° . tan 67°
= 1 x 1 = 1 = RHS.
L.H.S = R.H.S. सिद्ध हुआ।
दिखाइए कि:
cos 38° cos 52° - sin 38° sin 52° = 0.
LHS
= cos 38° . cos 52° - sin 38° . sin 52°
= cos (90° - 52°). cos 52° - sin (90° - 52°). sin 52°
= sin 52° . cos 52° - cos 52°. sin 52°
= 0 = RHS
L.H.S. = R.H.S.सिद्ध हुआ।
यदि tan 2A = cot (A - 18°), जहाँ एक न्यून कोण है, तो A का मान ज्ञान कीजिए।
tan 2A = cot (A - 18°)
[∵ cot (90° - θ) = tan θ]
⇒ cot (90° - 2A) = cot (A - 18°)
⇒ 90° - 2A = A - 18°
⇒ -3A = -108°
⇒ A = 36°.
यदि tan A = cot B, तो सिद्ध कीजिए कि A + B = 90°.
tan A = cot B
⇒ cot (90° - A) = cot B
⇒ 90° - A = B
⇒ 90° = A + B
अथवा A + B = 90°
यदि sec 4A = cosec (A - 20°), जहाँ 4A एक न्यून कोण है, तो A का मान बताओ।
हमें प्राप्त हैं:
sec 4A = cosec (A - 20°)
⇒ cosec (90° - 4A) = cosec (A - 20°)
[∵ cosec (90° - θ) = sec θ]
⇒ 90° - 4A = A - 20°
⇒ -5 A = -110°
⇒ A = 22°
sin67° + cos75° को 0° और 45° के बीच के कोणों के त्रिकोणमितीय अनुपातों के पदों में व्यक्त कीजिए।
sin 67° + cos 75°
= sin (90° - 23°) + cos (90° - 15°)

= cos 23° + sin 15°.
मान निकालिए:
![]()

sin (90° - 65°). cos 65° + cos (90° - 65°). sin 65°
= cos65°. cos 65° + sin 65°. sin 65°
= cos2 65° + sin2 65° [∵ sin2 A + cos2 A = 1]
= 1.
सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए:
9 sec2A - 9 tan2A बराबर हैं
-
1
-
9
-
8
-
0
1
9
8
0
B.
9
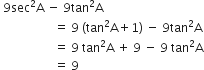
अत: विकल्प (B) सही हैं।
सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए:
 बराबर हैं:
बराबर हैं:
-
0
-
1
-
2
-
-1
0
1
2
-1
C.
2

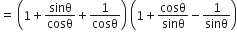
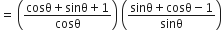
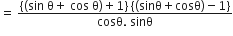
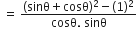
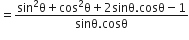
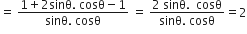
अत: विकल्प (C) सही हैं।
सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए:
(sec A + tan A) (1 - sin A) बराबर है:
-
sec A
-
sin A
-
cosec A
-
cos A
sec A
sin A
cosec A
cos A
D.
cos A
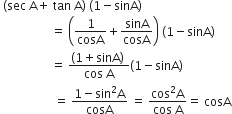
अत: विकल्प (D) सही हैं।
सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए:
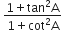 बराबर हैं:
बराबर हैं:
-

-
-1
-
cot2A
-
tan2A

-1
cot2A
tan2A
D.
tan2A
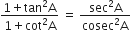
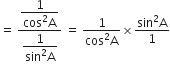
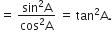
अत: विकल्प (D) सही हैं।
Sponsor Area
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:


L.H.S. =
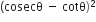
=
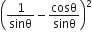
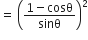
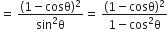
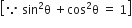
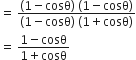
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
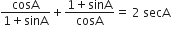
L.H.S. = 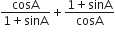
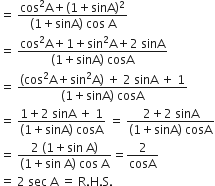
अत: L.H.S. = R.H.S.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
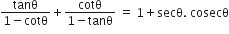
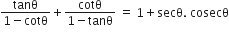
L.H.S. =
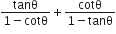

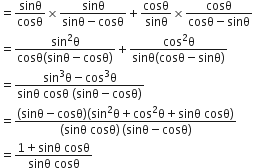
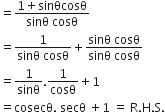
अत: L.H.S. = R.H.S.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
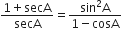
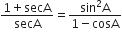
L.H.S. =

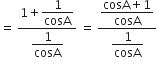
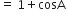
R.H.S. =
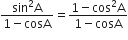

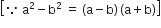
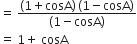
अत: L.H.S. = R.H.S.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
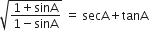

अत: L.H.S. = R.H.S.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
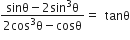
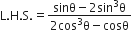
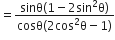
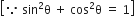

निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
(sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2A + cot2A
(sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2A + cot2 A
L.H.S. = (sin A + cosec A)2 + (cos A + sec A)2
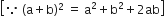
= (sin2 A + cosec2 A + 2 sin A. cosec A + cos2 A + sec2 A + 2 cos A. sec A
= (sin2 A + cos2 A) + 2 sin A. cosec A + 2 cos A. sec A + cosec2 A + sec2 A
= 1 + 2 + 2 + (cot2 A + 1) + (tan2 A + 1)
= 5 + 1 + 1 + cot2 A + tan2 A
= 7 + tan2 A + cot2 A = R.H.S.
अत: L.H.S. = R.H.S.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
(cosec A - sin A) (sec A - cos A) = 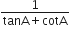
(cosec A - sin A) (sec A - cos A)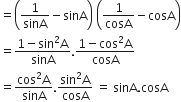
R.H.S. = 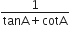
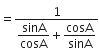
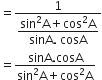

अत: L.H.S. = R.H.S.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
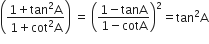
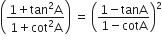
L.H.S. =
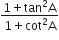
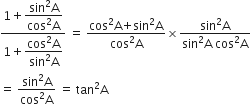
R.H.S. =
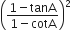
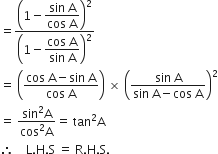
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
सर्वसमिका 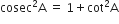 को लागू करके
को लागू करके
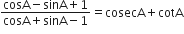
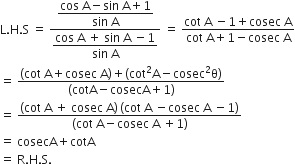
अत: L.H.S. = R.H.S.
(Cos267o - sin2 23o) का क्या मान है?
Cos2 67° - sin223°
cos (90° - θ) = sin θ
माना θ = 23°
cos (90° - 23°) = sin 23°
cos 67° = sin 23°
∴ cos267° = sin223°
∴ cos267° = sin223° = 0
यदि tan 2A = cot (A - 18o), जहाँ 2A एक न्यून कोण है, तो A का मान ज्ञात कीजिए।
मान लीजिये,
tan 2A = cot (A - 18o)
अब, हम जानते हैं कि,
tan θ = cot (90o - θ)
∴ cot (90o -2A) - cot (A -180)
∴ 900 - 2A = A - 180
∴ 3A = 1080
∴ A =1080 / 3 = 360
∴ A = 360
Mock Test Series
Sponsor Area
Sponsor Area






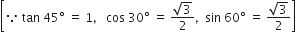

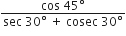
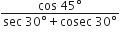
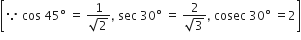
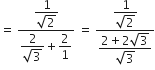
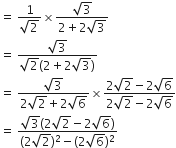
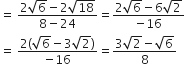
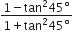
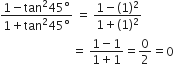
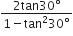 बराबर है।
बराबर है।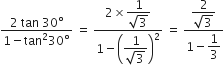
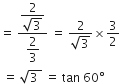

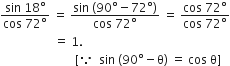

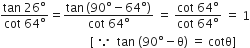

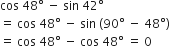

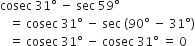
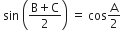

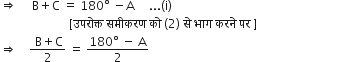
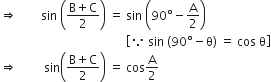
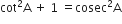

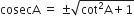
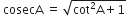



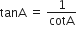
 के अन्य सभी त्रिकोणमितीय अनुपातों को sec A के पदों में लिखिए।
के अन्य सभी त्रिकोणमितीय अनुपातों को sec A के पदों में लिखिए।