निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
(cosec A - sin A) (sec A - cos A) = 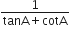$fraction numerator 1 over denominator tanA plus cotA end fraction$

Solution

(cosec A - sin A) (sec A - cos A)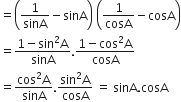
$equals open parentheses 1 over sinA minus sinA close parentheses space open parentheses 1 over cosA minus cosA close parentheses equals fraction numerator 1 minus sin squared straight A over denominator sinA end fraction. fraction numerator 1 minus cos squared straight A over denominator cosA end fraction equals fraction numerator cos squared straight A over denominator sinA end fraction. fraction numerator sin squared straight A over denominator cosA end fraction space equals space sinA. cosA$
R.H.S. = 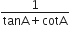$fraction numerator 1 over denominator tanA plus cotA end fraction$
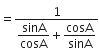
$equals fraction numerator 1 over denominator begin display style sinA over cosA end style plus begin display style cosA over sinA end style end fraction$
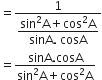
$equals fraction numerator 1 over denominator begin display style fraction numerator sin squared straight A plus cos squared straight A over denominator sinA. space cosA end fraction end style end fraction equals fraction numerator sinA. cosA over denominator sin squared straight A plus cos squared straight A end fraction$
$equals sinA. cosA$
अत: L.H.S. = R.H.S.

For Daily Free Study Material Join wiredfaculty

त्रिकोणमिति का परिचय

Some More Questions From त्रिकोणमिति का परिचय Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction