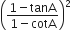
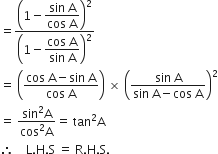त्रिकोणमिति का परिचय

Question

निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित हैं, न्यून कोण है:
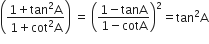
$open parentheses fraction numerator 1 plus tan squared straight A over denominator 1 plus cot squared straight A end fraction close parentheses space equals space open parentheses fraction numerator 1 minus tanA over denominator 1 minus cotA end fraction close parentheses squared equals tan squared straight A$

Solution

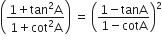
open parentheses fraction numerator 1 plus tan squared straight A over denominator 1 plus cot squared straight A end fraction close parentheses space equals space open parentheses fraction numerator 1 minus tanA over denominator 1 minus cotA end fraction close parentheses squared

L.H.S. =

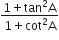
fraction numerator 1 plus tan squared straight A over denominator 1 plus cot squared straight A end fraction

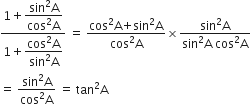
fraction numerator 1 plus begin display style fraction numerator sin squared straight A over denominator cos squared straight A end fraction end style over denominator 1 plus begin display style fraction numerator cos squared straight A over denominator sin squared straight A end fraction end style end fraction space equals space fraction numerator begin display style cos squared end style begin display style straight A end style begin display style plus end style begin display style begin display style sin end style squared end style begin display style straight A end style over denominator begin display style cos squared end style begin display style straight A end style end fraction cross times fraction numerator begin display style sin squared end style begin display style straight A end style over denominator begin display style sin squared end style begin display style straight A end style begin display style space end style begin display style begin display style cos end style squared end style begin display style straight A end style end fraction equals space fraction numerator begin display style sin squared end style begin display style straight A end style over denominator begin display style cos squared end style begin display style straight A end style end fraction space equals space tan squared straight A

R.H.S. =

open parentheses fraction numerator 1 minus tanA over denominator 1 minus cotA end fraction close parentheses squared

equals open parentheses 1 minus begin display style fraction numerator sin space straight A over denominator cos space straight A end fraction end style close parentheses squared over open parentheses 1 minus begin display style fraction numerator cos space straight A over denominator sin space straight A end fraction end style close parentheses squared equals space open parentheses fraction numerator cos space straight A minus sin space straight A over denominator cos space straight A end fraction close parentheses space cross times space open parentheses fraction numerator sin space straight A over denominator sin space straight A minus cos space straight A end fraction close parentheses squared equals space fraction numerator sin squared straight A over denominator cos squared straight A end fraction equals space tan squared straight A therefore space space space space straight L. straight H. straight S space equals space straight R. straight H. straight S.