Mathematics Chapter 9 Areas Of Parallelograms And Triangles
Sponsor Area
NCERT Solution For Class 9 About 2.html
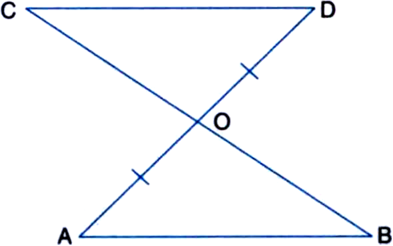
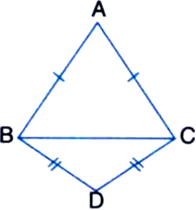
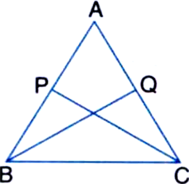
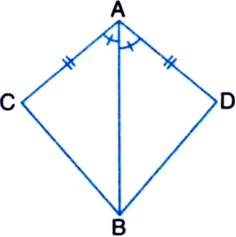
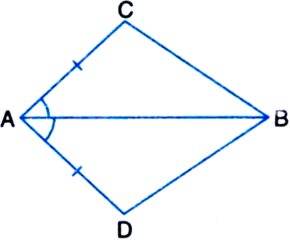
In quadrilateral ACBD, AC = AD and AB bisects ∠A (see figure). Show that ∆ABC ≅ ∆ABD. What can you say about BC and BD?
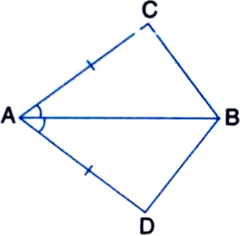
Given: In quadrilateral ACBD, AC = AD and AB bisects ∠A.
To Prove: ∆ABC ≅ ∆ABD.
Proof: In ∆ABC and ∆ABD,
AC = AD | Given
AB = AB | Common
∠CAB = ∠DAB
| ∵ AB bisects ∠A
∴ ∠ABC ≅ ∠ABD | SAS Rule
∴ BC = BD | C.P.C.T,
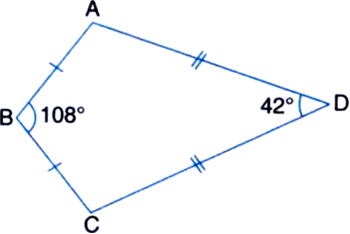
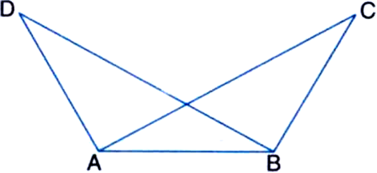
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see figure). Prove that:
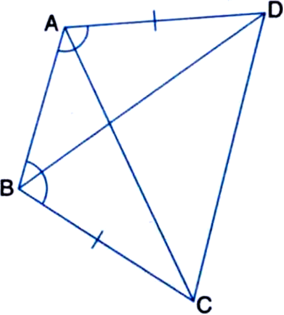
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
Given: ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA.
To Prove: (i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
Proof: (i) In ∆ABD and ∆BAC,
AD = BC | Given
AB = BA | Common
∠DAB = ∠CBA | Given
∴ ∆ABD ≅ ∠BAC | SAS Rule
(ii) ∵ ∆ABD ≅ ∆BAC | Proved in (i)
∴ BD = AC | C.P.C.T.
(iii) ∵ ∆ABD ≅ ∠BAC | Proved in (i)
∴ ∠ABD = ∠BAC. | C.P.C.T.
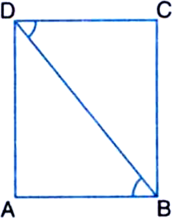
AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.
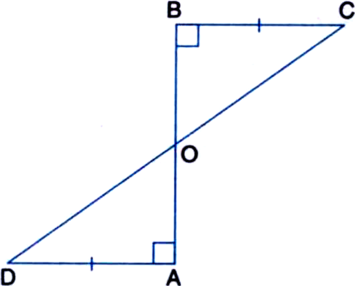
Given: AD and BC are equal perpendiculars to a line segment AB.
To Prove: CD bisects AB.
Proof: In ∆O AD and ∆OBC
AD = BC | Given
∠OAD = ∠OBC | Each = 90°
∠AOD = ∠BOC
| Vertically Opposite Angles
∴ ∠OAD ≅ ∆OBC | AAS Rule
∴ OA = OB | C.P.C.T.
∴ CD bisects AB.
I and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC ≅ ∆CDA.
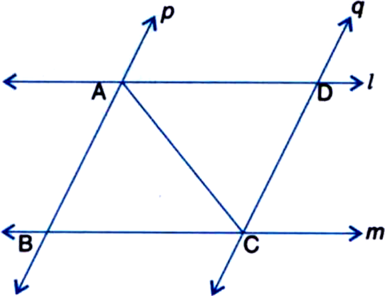
Given: I and m are two parallel lines intersected by another pair of parallel lines p and q.
To Prove: ∆ABC ≅ ∆CDA.
Proof: ∵ AB || DC
and AD || BC
∴ Quadrilateral ABCD is a parallelogram.
| ∵ A quadrilateral is a parallelogram if both the pairs of opposite sides are parallel
∴ BC = AD ...(1)
| Opposite sides of a ||gm are equal
AB = CD ...(2)
| Opposite sides of a ||gm are equal
and ∠ABC = ∠CDA ...(3)
| Opposite angles of a ||gm are equal
In ∆ABC and ∆CDA,
AB = CD | From (2)
BC = DA | From (1)
∠ABC = ∠CDA | From (3)
∴ ∆ABC ≅ ∆CDA. | SAS Rule
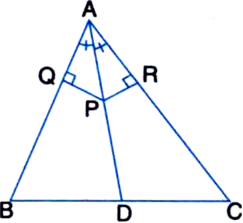
Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.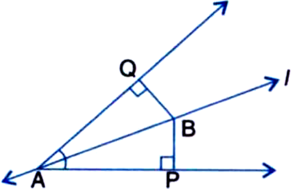
Given: Line l is the bisector of an angle A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A.
To Prove: (i) ∆APB ≅ ∆AQB
(ii) BP = BQ
Or
B is equidistant from the arms of ∠A.
Proof: (i) In ∆APB and ∆AQB,
∠BAP = ∠BAQ
| ∵ l is the bisector of ∠A
AB = AB | Common
∠BPA = ∠BQA | Each = 90°
| ∵ BP and BQ are perpendiculars from B to the arms of ∠A
∴ ∆APB ≅ ∆AQB | AAS Rule
(ii) ∵ ∆APB ≅ ∆AQB
| Proved in (i) above
∴ BP = BQ. | C.P.C.T.
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
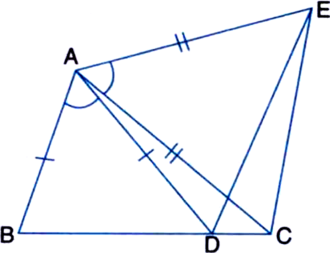
Given: In figure, AC = AE, AB = AD and ∠BAD = ∠EAC.
To Prove: BC = DE.
Proof: In ∆ABC and ∆ADE,
AB = AD | Given
AC = AE | Given
∠BAD = ∠EAC | Given
⇒ ∠BAD + ∠DAC = ∠DAC + ∠EAC
| Adding ∠DAC to both sides
⇒ ∠BAC = ∠DAE
∴ ∆ABC ≅ ∆ADE | SAS Rule
∴ BC = DE. | C.P.C.T.
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.
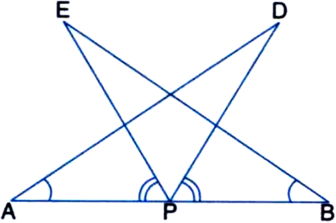
Given: AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB.
To Prove: (i) ∆DAP ≅ ∆EBP
(ii) AD = BE.
Proof: (i) In ∆DAP and ∆EBP,
AP = BP
| ∵ P is the mid-point of the line segment AB
∠DAP = ∠EBP | Given
∠EPA = ∠DPB | Given
⇒ ∠EPA + ∠EPD = ∠EPD + ∠DPB
| Adding ∠EPD to both sides
⇒ ∠APD = ∠BPE
∴ ∠DAP ≅ ∠EBP | ASA Rule
(ii) ∵ ∆DAP ≅ AEBP | From (i) above
∴ AD = BE. | C.P.C.T.
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that:
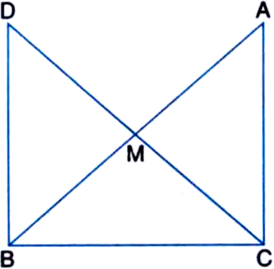
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB![]()
Given: In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B.
To Prove: (i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∠DBC ≅ ∆ACB![]()
(i) In ∆AMC and ∆BMD,
AM = BM
| ∵ M is the mid-point of the hypotenuse AB
CM = DM | Given
∠AMC = ∠BMD
| Vertically Opposite Angles
∴ ∆AMC ≅ ∆BMD. | SAS Rule
(ii) ∵ ∆AMC ≅ ∆BMD
| From (i) above
∠ACM = ∠BDM | C.P.C.T.
But these are alternate interior angles and they are equal
∴ AC || BD
Now, AC || BD and a transversal BC intersects them
∴ ∠DBC + ∠ACB = 180°
| ∵ The sum of the consecutive interior angles on the same side of a transversal is
180°
⇒ ∠DBC + 90° = 180°
| ∵ ∠ACB = 90° (given)
⇒ ∠DBC = 180° - 90° = 90°
⇒ ∠DBC is a right angle.
(iii) In ∆DBC and ∆ACB,
∠DBC = ∠ACB (each = 90°)
| Proved in (ii) above
BC = CB | Common
∵ ∆AMC ≅ ∆BMD | Proved in (i) above
∴ AC = BD | C.P.C.T.
∴ ∆DBC ≅ ∆ACB. | SAS Rule
(iv) ∵ ∆DBC ≅ ∆ACB
| Proved in (iii) above
∴ DC = AB | C.P.C.T.![]() 2CM = AB
2CM = AB
![]()
![]()
In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.
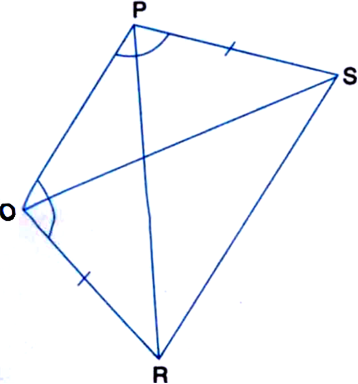
In ∆QPR and ∆PQS,
QR = PS | Given
∠RQP = ∠SPQ | Given
PQ = PQ | Common
∴ ∆QPR ≅ ∆PQS | SAS Axiom
∴ PR = QS | C.P.C.T.
and ∠QPR = ∠PQS. | C.P.C.T.
In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.
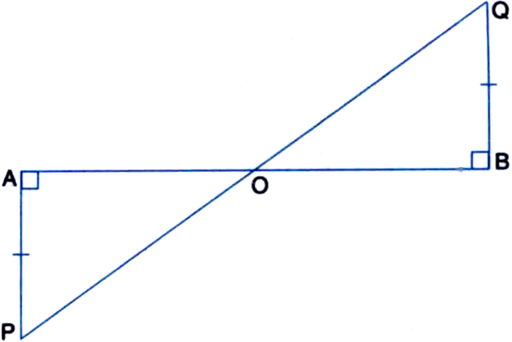
In ∆OAP and ∆OBQ,
AP = BQ | Given
∠OAP = ∠OBQ | Each = 90°
∠AOP = ∠BOQ
| Vertically Opposite Angles
∴ ∆OAP ≅ ∆OBQ | AAS Axiom
∴ OA = OB | C.P.C.T.
and OP = OQ | C.P.C.T.
⇒ O is the mid-point of line segments AB and PQ
In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.
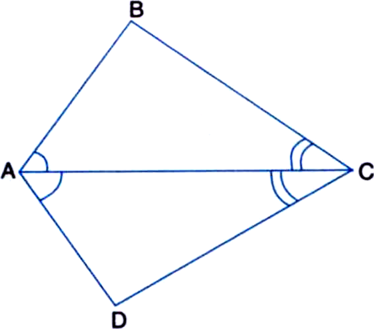
In ∆ABC and ∆ADC,
∠BAC = ∠DAC | Given
∠ACB = ∠ACD | Given
AC = AC | Common
∴ ∆ABC ≅ ∆ADC | ASA Axiom
∴ AB = AD | C.P.C.T.
and CB = CD. | C.P.C.T.
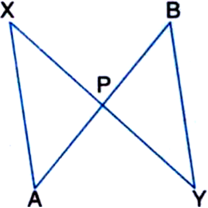
AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.
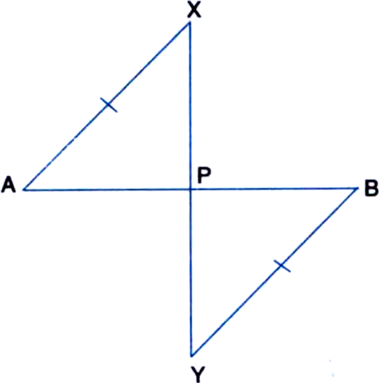
(i) ∵ AX || BY and AB intersects them
∴ ∠PAX = ∠PBY ...(1)
| Alternate Angles
∵ AX || BY and XY intersects them
∴ ∠PXA = ∠PYB ...(2)
| Alternate Angles
In ∆APX and ∆BPY,
∠PAX = ∠PBY | From (1)
∠PXA = ∠PYB | From (2)
AX = BY | Given
∴ ∆APX = ∆BPY | ASA Axiom
(ii) ∵ AP = BP | C.P.C.T.
and PX = PY | C.P.C.T.
⇒ AB and XY bisect each other at P.
In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.
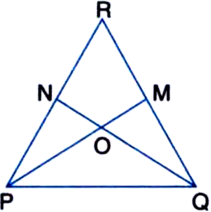
Given: ∠QPR = ∠PQR and M and N are respectively points on side QR and PR of ∆PQR, such that QM = PN.
To Prove: OP = OQ, where O is the point of intersection of PM and QN.
Proof: In ∆PNQ and ∆QMP,
PN = QM | Given
PQ = QP | Common
∠QPN = ∠PQM | Given
∴ ∆PNQ ≅ ∆QMP
| SAS congruence rule
∴ ∠PNQ = ∠QMP | CPCT
Again, in ∆PNO and ∆QMO,
PN = QM | Given
∠PON = ∠QOM
| Vertically opposite angles
∠PNO = ∠QMO | Proved above
∴ ∆PNO ≅ ∆QMO
| AAS congruence rule
∴ OP = OQ | CPCT
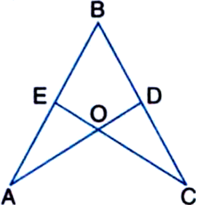
Prove that the medians of an equilateral triangle are equal.
Given: ABC is an equilateral triangle whose medians are AD, BE and CF.
To Prove: AD = BE = CF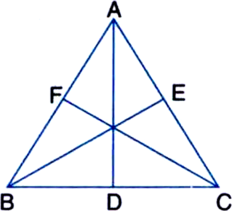
Proof: In ∆ADC and ∆BEC,
AC = BC
![]()
![]()
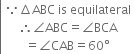
DE = EC
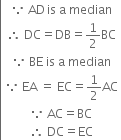
![]()
| SAS congruence rule![]()
![]() ....(1) | CPCT
....(1) | CPCT
Similarly, we can prove that
BE = CF ...(2)
and CF = AD ...(3)
From (1), (2) and (3)
AD = BE = CF
In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.
Given: In figure,
∠B = ∠E, BD = CE
and ∠1 = ∠2
To Prove: ∆ABC ≅ ∆AED
Proof: ∠1 = ∠2
⇒ ∠1 + ∠DAC = ∠2 + ∠DAC
⇒ ∠BAC = ∠EAD ...(1)
BD = CE
⇒ BD + DC = CE + DC
⇒ BC = ED ...(2)
∠B = ∠E ...(3)
In view of (1), (2) and (3),
∆ABC ≅ ∆AED
| AAS congruence rule
In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.
Given: AD is the median of ∆ABC. BE ⊥ AD, CF ⊥ AD.
To Prove: BE = CF
Proof: In ∆DEB and ∆DFC,
DB = DC
| ∵ AD is the median of ∆ABC
∠DEB = ∠DFC | Each = 90°
∠BDE = ∠CDF
| Vertically opposite angles
∴ ∆DEB ≅ ∆DFC
| AAS congruence rule
∴ BE = CF | CPCT
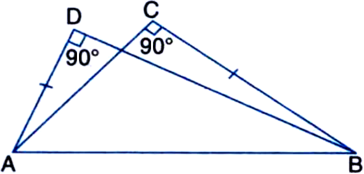
In the given figure, if AB = FE, BC = ED, AB ⊥ BD and FE ⊥ EC, then prove that AD = FC.
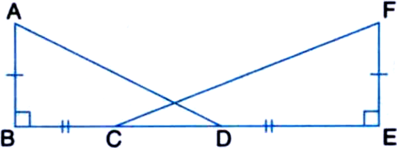
Given:
AB = FE, BC = ED,
AB ⊥ BD and FE ⊥ EC
To Prove: AD = FC
Proof: In ∆ABD and ∆FEC,
AB = FE ...(1) | Given
∠ABD = ∠FEC ...(2)
| Each = 90°
BC = ED | Given
⇒ BC + CD = ED + DC
⇒ BD = EC ...(3)
In view of (1), (2) and (3),
∆ABD ≅ ∆FEC
| SAS congruence rule
∴ AD = FC | CPCT
Sponsor Area
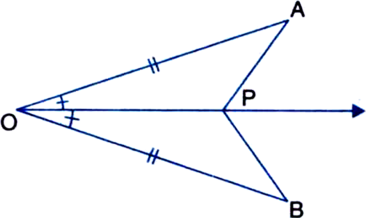
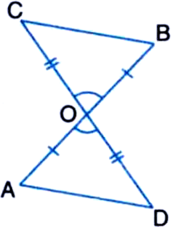
In figure, OA = OB and OD = OC. Show that:
(i) ∆AOD ≅ ∆BOC and (ii) AD = BC.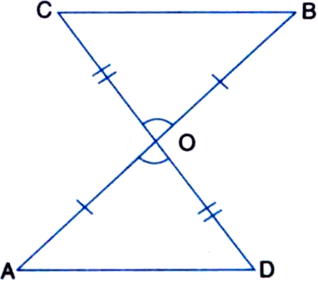
Solution not provided.
AB is a line segment and line l is its perpendicular bisector. If a point P lies on I, show that P is equidistant from A and B.
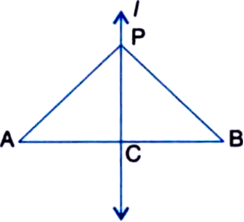
Solution not provided.
In the figure, ∠BCD = ∠ADC and ∠ACB = ∠BDA. Prove that AD = BC and ∠A = ∠B.
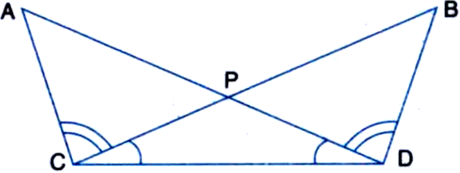
Solution not provided.
In the figure given below, ABCD is a quadrilateral in which diagonal AC bisects ∠A and ∠C, prove that ∆ABC ≅ ∆ADC.
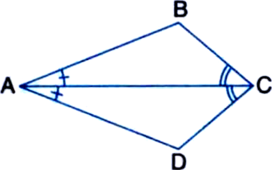
Solution not provided.
In the figure below, the diagonal AC of quadrilateral ABCD bisects ∠BAD and ∠BCD. Prove that BC = CD.
Solution not provided.
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects ∠A.
Given: In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O.
To Prove: (i) OB = OC
(ii) AO bisects ∠A.
Proof: (i) AB = AC | Given
∴ ∠B = ∠C
| Angles opposite to equal sides of a triangle are equal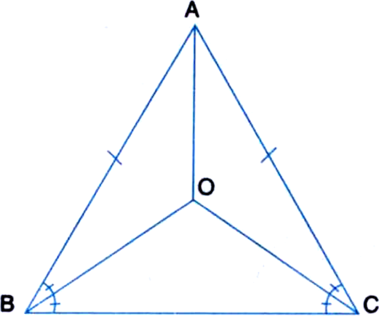
![]()
∴ ∠OBC = ∠OCB
| ∵ BO and CO are the bisectors of ∠B and ∠C respectively
∴ OB = OC
| Sides opposite to equal angles of a triangle are equal
(ii) In ∆OAB and ∆OAC,
AB = AC | Given
OB = OC | Proved in (i) above
OA = OA | Common
∴ ∠B = ∠C
| Angles opposite to equal sides of a triangle are equal![]()
∴ ∠ABO = ∠ACO
| ∵ BO and CO are the bisectors of ∠B and ∠C respectively
∴ ∆OAB ≅ ∆OAC | By SAS Rule
∴ ∠OAB = ∠OAC | C.P.C.T.
∴ AO bisects ∠A.
In ∆ ABC, AD is the perpendicular bisector of BC (see figure). Show that A ABC is an isosceles triangle in which AB = AC.

Given: In ∆ ABC, AD is the perpendicular bisector of BC.
To Prove: A ABC is an isosceles triangle in which AB = AC.
Proof: In ∆ ADB and ∆ADC,
∠ADB = ∠ADC | Each = 90° DB = DC
| ∵ AD is the perpendicular bisector of BC
AD = AD | Common
∴ ∆DB ≅ ∆ADC | By SAS Rule
∴ AB = AC | C.P.C.T.
∴ ∆ABC is an isosceles triangle in which AB = AC.
ABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively (see figure). Show that these altitudes are equal.
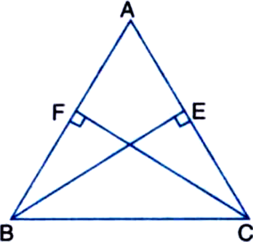
Given: ABC is an isosceles triangle in which altitudes BE and CF are drawn to sides AC and AB respectively.
To Prove: BE = CF.
Proof: ∵ ABC is an isosceles triangle
∴ AB = AC
∴ ∠ABC = ∠ACB ...(1)
| Angles opposite to equal sides of a triangle are equal
In ∆BEC and ∆CFB,
∠BEC = ∠CFB | Each = 90°
BC = CB | Common
∠ECB = ∠FBC | From (1)
∴ ∆BEC ≅ ∆CFB | By AAS Rule
∴ BE = CF. | C.P.C.T.
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that:
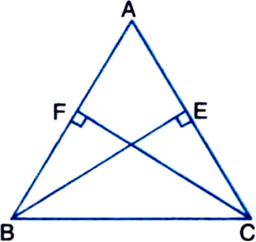
(i) ∆ABE ≅ ∆ACF
(ii) AB = AC, i.e., ∆ABC is an isosceles triangle.
Given: ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal.
To Prove: (i) ∆ABE = ∆ACF
(ii) AB = AC, i.e., ∆ABC is an isosceles triangle.
Proof: (i) In ∆ABE and ∆ACF
BE = CF | Given
∠BAE = ∠CAF | Common
∠AEB = ∠AFC | Each = 90°
∴ ∆ABE ≅ ∆ACF | By AAS Rule
(ii) ∆ABE ≅ ∆ACF | Proved in (i) above
∴ AB = AC | C.P.C.T.
∴ ∆ABC is an isosceles triangle.
ABC and DBC are two isosceles triangles on the same base BC (see figure). Show that ∠ABD = ∠ACD.
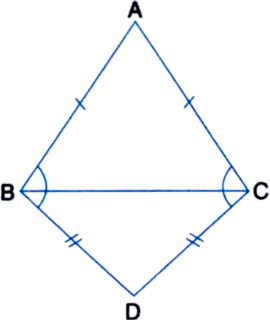
Given: ABC and DBC are two isosceles triangles on the same base BC.
To Prove: ∠ABD = ∠ACD.
Proof: ∵ ABC is an isosceles triangle on the base BC.
∴ ∠BC = ∠ACB ...(1)
∵ DBC is an isosceles triangle on the base BC
∴ ∠DBC = ∠DCB ...(2)
Adding the corresponding sides of (1) and (2), we get
∠ABC + ∠DBC = ∠ACB + ∠DCB
⇒ ∠ABD = ∠ACD.
∆ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∆BCD is a right angle.
Given: ∆ABC is an isosceles triangle in which AB = AC.
Side BA is produced to D such that AD = AB.
To Prove: ∠BCD is a right angle.
Proof: ∵ ABC is an isosceles triangle
∴ ∠ABC = ∠ACB ...(1)
∵ AB = AC and AD = AB
∴ AC = AD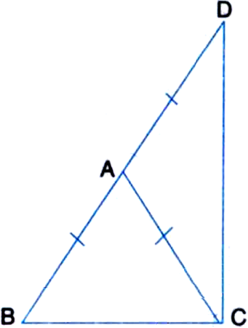
∴ In ∆ACD,
∠CDA = ∠ACD
| Angles opposite to equal sides of a triangle are equal
⇒ ∠CDB = ∠ACD ...(2)
Adding the corresponding sides of (1) and (2), we get
∠ABC + ∠CDB = ∠ACB + ∠ACD
⇒ ∠ABC + ∠CDB = ∠BCD ...(3)
In ∆BCD,
∠BCD + ∠DBC + ∠CDB = 180°
| ∵ Sum of all the angles of a triangle is 180°
⇒ ∠BCD + ∠ABC + ∠CDB = 180°
⇒ ∠BCD + ∠BCD = 180°
| Using (3)
⇒ 2∠BCD = 180°
⇒ ∠BCD = 90°
⇒ ∠BCD is a right angle.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
∵ In ∆ABC,
AB = AC
∴ ∠B = ∠C ...(1)
| Angles opposite to equal sides of a triangle are equal
In ∆ABC,
∠A + ∠B + ∠C = 180°
| Sum of all the angles of a triangle is 180°
⇒ 90° + ∠B + ∠C = 180°
| ∵ ∠A = 90° (given)
⇒ ∠B + ∠C = 90° ...(2)
From (1) and (2), we get
∠B = ∠C = 45°.
Show that the angles of an equilateral triangle are 60° each.
Given: An equilateral triangle ABC.
To Prove: ∠A = ∠B = ∠C = 60°.
Proof: ∵ ABC is an equilateral triangle
∴ AB = BC = CA ...(1)
∵ AB = BC
∴ ∠A = ∠C ...(2)
| Angles opposite to equal sides of a triangle are equal
∵ BC = CA
∴ ∠A = ∠B ...(3)
| Angles opposite to equal sides of a triangle are equal
From (2) and (3), we obtain
∠A = ∠B = ∠C ...(4)
In ∆ABC,
∠A + ∠B + ∠C = 180° ...(5)
| Sum of all the angles of a triangle is 180°
Let ∠A = x°. Then, ∠B = ∠C = x°
| From (4)
From (5),
x° + x° + x° = 180°
3x° = 180°
⇒ x° = 60°
⇒ ∠A = ∠B = ∠C = 60°.
Angles A, B and C of a triangle ABC are equal to each other. Prove that ∆ABC is equilateral.
∵ ∠A = ∠B
∴ BC = CA ...(1)
| Sides opposite to equal angles of ∆ABC
∵ ∠B = ∠C
∴ CA = AB ...(2)
| Sides opposite to equal angles of ∆ABC
∵ ∠C = ∠A
∴ AB = BC ...(3)
| Sides opposite to equal angles of ∆ABC
From (1), (2) and (3), we have
AB = BC = CA
⇒ ∆ABC is equilateral.
BD and CE are the bisectors of ∠B and ∠C of an isosceles triangle ABC with AB = AC. Prove that BD = CE.
∵ AB = AC
∴ ∠ACB = ∠ABC
| Angles opposite to equal sides of ∆ABC
⇒ 2∠2 = 2∠1
| ∵ CE and BD are the bisectors of ∠C and ∠B respectively
⇒ ∠2 = ∠1
⇒ BP = PC ...(1)
| Sides opposite to equal angles of ∆PBC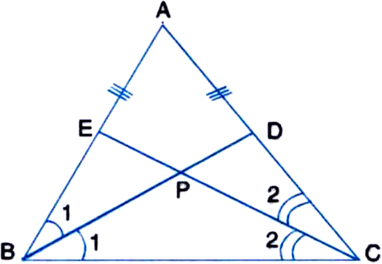
In ∆BPE and ∆CPD,
BP = CP | Proved above
∠EBP = ∠DCP | Proved above
∠BPE = ∠CPD
| Vertically Opposite Angles
∴ ∆BPE ≅ ∆CPD | ASA Axiom
PE = PD | C.P.C.T.
⇒ PD = PE ...(2)
Adding (1) and (2), we get
BP + PD = PC + PE
⇒ BD = CE.
ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that AD bisects ∠BAC and AB = CD. Prove that ∠BAC = 72°.
[Hint. Take a point P on AC such that BP bisects ∠B. Join P and D.]
Construction: Take a point P on AC such that BP bisects ∠B. Join P and D.
Proof: In ∆ABC,
∵ BP bisects ∠ABC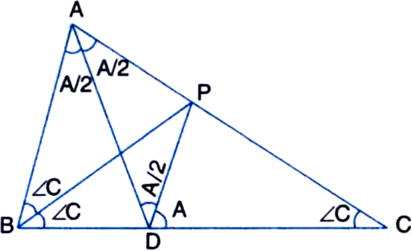
![]()
In APBC,
∴ ∠PBC = ∠PCB (= ∠C)
∴ PB = PC ...(2)
| Sides opposite to equal angles of∆PBC In ∆APB and ∆DPC,
AB = CD | Given
PB = PC | From (2)
∠ABP = ∠DCP (= ∠C)
∴ ∆APB ≅ ∆DPC | SAS Axiom
∴ ∠BAP = ∠CDP (= ∠A) ...(3)
| C.P.C.T.
and AP = DP ...(4) | C.P.C.T.
In ∆APD,
∵ AP = DP | From (4)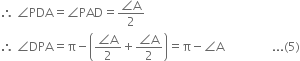
Again from ∆DPC,
∠DPC = π - (∠A + ∠C)
∴ ∠DPA = π - ∠DPC = π - {π - (∠A + ∠C)} = ∠A + ∠C ...(6)
From (5) and (6),
π - A = ∠A + ∠C ⇒ 2∠A + ∠C = π ...(7)
Again,
∠A + ∠B + ∠C = π
| ∵ The sum of three angles of ∆ABC = π ⇒ ∠A + 2∠C + ∠C = π | ∵ ∠B = 2∠C
⇒ ∠A + 3∠C = π ...(8)
Multiplying (7) by 3, we get
6∠A + 3∠C = 3π ...(9)
Subtracting (8) from (9), we get
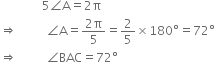
Suppose line segments AB and CD intersect at O in such a way that AO = OD and OB = OC. Prove that AC = BD but AC may not be parallel to BD.
In ∆OAC and ∆ODB,
OA = OD | Given
OB = OC | Given
∠AOC = ∠DOB
| Vertically Opposite Angles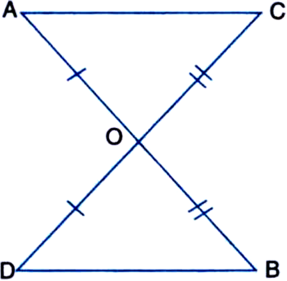
∴ ∆OAC ≅ ∆ODB | SAS Axiom
∴ AC = BD | C.P.C.T.
Also, ∠OAC = ∠ODB | C.P.C.T.
and ∠OCA = ∠OBD | C.P.C.T.
Thus ∠OAC may not be equal to ∠OBD and therefore, AC may not be parallel to BD
However, if OA = OC, then ∠OAC = ∠OCA
| Angles opposite to equal sides of ∆OAC But ∠OAC = ∠ODB
∴ ∠OCA = ∠ODB
But these angles form a pair of equal alternate angles
∴ AC || BD.
Sponsor Area
In the figure, D and E are points on the base BC of a ∆ABC such that AD = AE and ∠BAD = ∠CAE. Prove that AB = AC.
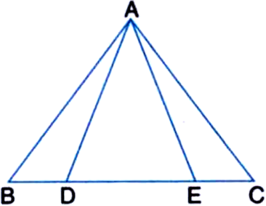
Given: D and E are points on the base BC of a ∆ABC such that AD = AE and ∠BAD = ∠CAE.
To Prove: AB = AC
Proof: In ∆ADE,
∵ AD = AE | Given
∴ ∠ADE = ∠AED ...(1)
| Angles opposite to equal sides of a triangle are equal
In ∆ABD,
Ext. ∠ADE = ∠BAD + ∠ABD ...(2)
| An exterior angle of a triangle is equal to the sum of its two interior opposite angles
In ∆AEC,
Ext. ∠AED = ∠CAE + ∠ACE .. .(3)
| An exterior angle of a triangle is equal to the sum of its two interior opposite angles
From (1), (2) and (3),
∠BAD + ∠ABD = ∠CAE + ∠ACE
⇒ ∠ABD = ∠ACE
| ∵ ∠BAD = ∠CAE (Given)
⇒ ∠ABC = ∠ACB
∴ AB = AC
| Sides opposite to equal angles of a triangle are equal
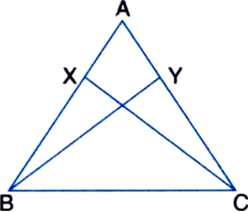
In figure, X and Y are two points on equal sides AB and AC of a ∆ABC such that AX = AY. Prove that XC = YB.
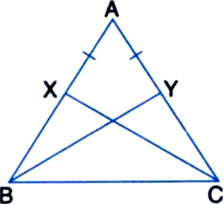
Given: X and Y are two points on equal sides AB and AC of a ∆ABC such that AX = AY.
To Prove: XC = YB
Proof: In ∆ABC,
∵ AB = AC | Given
∴ ∠ABC = ∠ACB ...(1)
| Angles opposite to equal sides of a triangle are equal
Again, AB = AC | Given
AX = AY | Given
Subtracting, we get,
AB - AX = AC - AY
⇒ BX = CY ...(2)
In ∆BXC and ∆CYB,
BX = CY | From (2)
BC = CB | Common
∠XBC = ∠YCB | From (1)
∴ ∆BXC ≅ ∆CYB
| SAS congruence rule
∴ XC = YB | CPCT
Prove that the angles opposite to equal sides of a triangle are equal. Is the converse true?
Given: A triangle ABC in which AB = AC
To Prove: ∠ABC = ∠ACB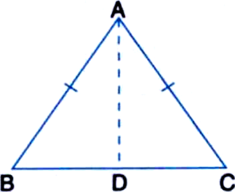
Construction: Draw the bisector AD of A so as to intersect BC at D.
Proof: In ∆ADB and ∆ADC,
AD = AD | Common
AB = AC | Given
∠BAD = ∠CAD
| By Construction
∴ ∆ADB ≅ ∆ADC
| SAS congruence rule
∴ ∠ABD = ∠ACD | CPCT
⇒ ∠ABC = ∠ACB
Yes, the converse is true.
In figure, AB = AC, D is the point in the interior of ∆ABC such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ∆ABC.
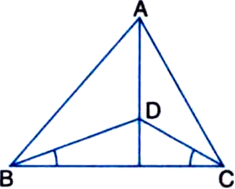
Given: AB = AC, D is the point in the interior of ∆ABC such that ∠DBC = ∠DCB.
To Prove: AD bisects ∠BAC of ∆ABC.
Proof: In ∆DBC,
∵ ∠DBC = ∠DCB ...(1) | Given
∴ DB = DC ...(2)
| Sides opposite to equal angles of a triangle are equal
In ∆ABC,
∵ AB = AC | Given
∴ ∠ABC = ∠ACB
∴ ∠ABC = ∠ACB ...(3)
| Angles opposite to equal sides of a triangle are equal
Subtracting (1) from (3), we get,
∠ABC - ∠DBC = ∠ACB - ∠DCB
⇒ ∠ABD = ∠ACD ...(4)
In ∆ADB and ∆ADC,
AB = AC | Given
DB = DC | Proved in (2)
∠ABD = ∠ACD | Proved in (4)
∴ ∆ADB ≅ ∆ADC
| SAS congruence rule
∴ ∠DAB = ∠DAC | CPCT
⇒ AD bisects ∠BAC of ∆ABC.
In figure, ABCD is a square and ∠DEC is an equilateral triangle. Prove that
(i) ∆ADE ≅ ∆BCE
(ii) AE = BE
(iii) ∠DAE = 15°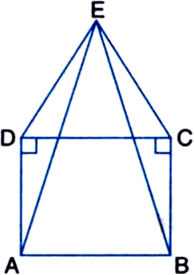
Given: ABCD is a square and ∆DEC is an equilateral triangle.
To Prove:
(i) ∆ADE ≅ ∆BCE
(ii) AE = BE
(iii) ∠DAE = 15°
Proof: (i) In ∆ADE and ∆BCE,
AD = BC
![]()
DE=CE
![]()
∴ ∆ADE ≅ ∆BCE | SAS congruence rule
(ii) ∵ ∆ADE ≅ ∆BCE | Proved in (1)
∴ AE = BE | CPCT
(iii) In ∆DAE,
∵ DE = DA | Given
∴ ∠DAE = ∠DEA ...(1)
| Angles opposite to equal sides of a triangle are equal Also, ∠ADE + ∠DAE + ∠DEA = 180°
| Angle sum property of a triangle
⇒ (∠ADC + ∠EDC) + ∠DAE + ∠DEA = 180°
⇒ (90° + 60°) + ∠DAE + ∠DEA = 180°
⇒ ∠DAE + ∠DEA = 30° ...(2)
From (1) and (2),
∠DAE = 15° = ∠DEA
In ∆ABC, AB = AC, ∠A = 36°. If the internal bisector of ∠C meets AB at D, Prove that AD = DC.
Given: In ∆ABC, AB = AC, ∠A = 36°. The internal bisector of ∠C meets AB at D.
To Prove: AD = DC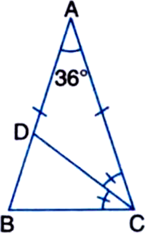
Proof: In ∆ABC,
∵ AB = AC
∴ ∠ABC = ∠ACB ...(1)
| Angles opposite to equal sides of a triangle are equal
Also, ∠BAC + ∠ABC + ∠ACB = 180°
| Angle sum property of a triangle
⇒ 360° + ∠ABC + ∠ACB = 180°
⇒ ∠ABC + ∠ACB = 144° ...(2)
From (1) and (2),
![]()
Now, ∵ CD bisects ∠ACB
![]()
Again, In ∆ACD,
∠ACD = ∠CAD (= 36°)
∴ AD = DC
| Sides opposite to equal angles of a triangle are equal
In figure, AB = BC, AD = EC. Prove that ∆ABE ≅ ∆CBD.
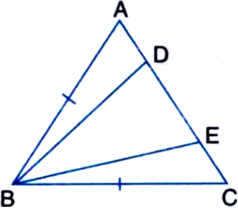
Given: AB = BC, AD = EC
To Prove: ∆ABE ≅ ∆CBD
Proof: In ∆ABC,
∵ AB = BC | Given
∴ ∠BAC = ∠BCA ...(1)
| Angles opposite to equal sides of a triangle are equal
AD = EC | Given
⇒ AD + DE = EC + DE
⇒ AE = CD ...(2)
Now, in ∆ABE and ∆CBD,
AE = CD | From (2)
AB = CB | Given
∠BAE = ∠BCD | From (1)
∴ ∆ABE ≅ ∆CBD | SAS congruence rule.
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC. Show that ∠B = ∠C.
Given: ABC is an isosceles triangle with
AB = AC.
AP ⊥ BC
To Prove: ∠B = ∠C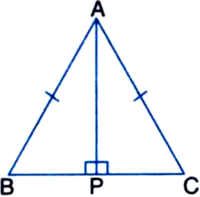
Proof: In ∆ABC,
∵ AB = AC | Given
∴ ∠ABC = ∠ACB ...(1)
| Angles opposite to equal sides of a triangle are equal
Now, in ∆APB and ∆APC,
AB = AC | Given
∠ABP = ∠ACP | From (1)
∠APB = ∠APC (= 90°) | Given
∴ ∆APB ≅ ∆APC | AAS congruence rule
∴ ∠ABP = ∠ACP | CPCT
⇒ ∠B = ∠C
In an isosceles triangle ABC with AB = AC, BD and CE are two medians. Prove that BD = CE.
Given: In an isosceles triangle ABC with AB = AC, BD and CE are two medians.
To Prove: BD = CE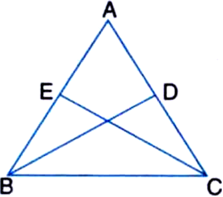
Proof: In ∆ABC,
∵ AB = AC
∴ ∠BC = ∠ACB ...(1)
| Angles opposite to equal sides of a triangle are equal
Also, ![]()
| Halves of equals are equal ⇒ BE = CD ...(2)
| ∵ BD and CE are two medians
Now, in ∆BDC and ∆CEB,
∠BCD = ∠CBE | From (1)
BE = CD | From (2)
BC = CB | Common
∴ ∆BDC ≅ ∆CEB
| SAS congruence rule
∴ BD = CE | CPCT
In figure, ∠x = ∠y and PQ = PR. Prove that PE = RS.
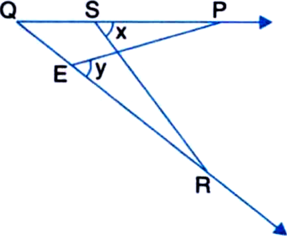
Given: In figure, ∠x = ∠y and PQ = PR
To Prove: PE = RS
Construction: Join PR
Proof: In ∆PQR,
∵ PQ = QR | Given
∴ ∠QRP = ∠QPR
| Angles opposite to equal sides of a triangle are equal
⇒ ∠ERP = ∠SPR ...(1)
In ∆PER and ∆RSP,
∠ERP = ∠SPR From (1)
∠REP = ∠PSR | Given
PR = RP | Common
∴ ∆PER ≅ ∆RSP
| AAS congruence rule
∴ PE = RS | CPCT
In the given figure, AE bisects ∠DAC and ∠B = ∠C, prove that AE || BC.
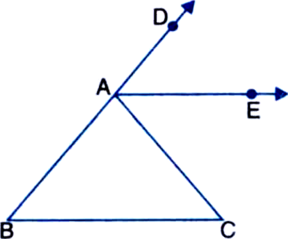
Given: AE bisects ∠DAC and ∠B = ∠C
To Prove: AE || BC
Proof: In ∆ABC,
Ext. ∠DAC = ∠ABC + ∠ACB ...(1)
| An exterior angle of a triangle is equal to the sum of its two interior opposite angles
⇒ ∠DAC = ∠ACB + ∠ACB
| ∵ ∠B = ∠C (Given)
⇒ ∠DAC = 2∠ACB
⇒ 2∠CAE = 2∠ACB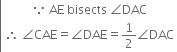
⇒ ∠CAE = ∠ACB
But these angles form a pair of equal alternate interior angles
∴ AE || BC
If the bisector of the vertical angle of a triangle bisects the base of the triangle, then prove that the triangle is isosceles.
Given: A ∆ABC in which the bisector of the vertical angle ∠BAC bisects the base BC, i.e., BD = CD
To Prove: ∆ABC is isosceles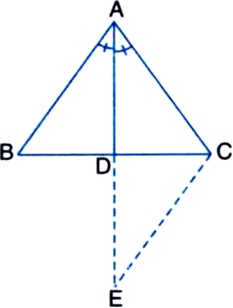
Construction: Produce AD to E such that AD = DE. Join EC.
Proof: In ∆ADB and ∆EDC,
BD = CD | Given
AD = ED | By construction
∠ADB = ∠EDC
| Vertically opposite angles
∴ ∆ADB ≅ ∆EDC
| SAS congruence rule ∴ AB = EC ...(1) | CPCT
and ∠BAD = ∠CED | CPCT
But ∠BAD = ∠CAD | Given
∴ ∠CAD = ∠CED
∴ AC = CE ...(2)
| Sides opposite to equal angles of a triangle are equal
From (1) and (2),
AB = AC
∴ ∆ABC is isosceles.
In figure, ∠BAC = 85°, ∠A - ∠B and BD = CD. Find the measure of ∠x, ∠y and ∠z. Give reasons to support your answer.
In ∆ABC,
∵ ∠A = ∠B | Given
∴ ∠CAB = ∠CBA (= 85°)
| Angles opposite to equal sides of a triangle are equal
Also, x + ∠CAB + ∠CBA = 180°
| Angle sum property of a triangle
⇒ x + 85° + 85° = 180°
⇒ x = 10°
In ∆BCD,
∵ BD = CD
∴ x = z = 10°
| Angles opposite to equal sides of a triangle are equal
Also, z + x + y = 180°
| Angle sum property of a triangle
⇒ 10° + 10° + y = 180°
⇒ y = 160°
In ∆ABC, the bisector AD of ∠A is perpendicular to side BC (see figure). Show that AB = AC and ∆ABC is isosceles.
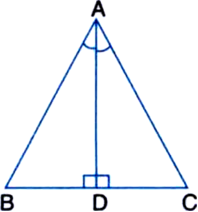
Solution not provided.
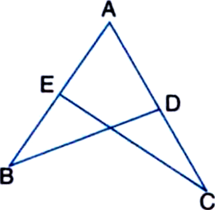
E and F are respectively the mid-points of equal sides AB and AC of ∆ABC (see figure). Show that BF = CE.
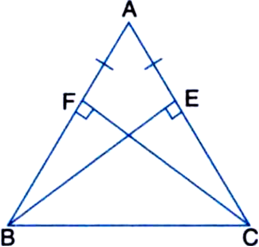
Solution not provided.
In an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD (see figure). Show that AD = AE.
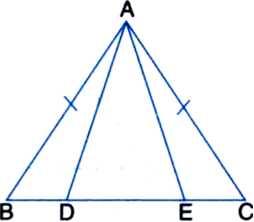
Solution not provided.
AD and BE are respectively the altitudes of an isosceles triangle ABC. in which AC = BC. Prove that AE = BD.
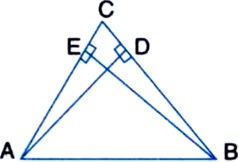
Solution not provided.
PS is an altitude of an isosceles triangle PQR in which PQ = PR. Show that PS bisects ∠P.
Solution not provided.
In ∆ABC, AB = AC. D is a point in side ∆ABC such that BD = DC. Prove that ∠ABD = ∠ACD.
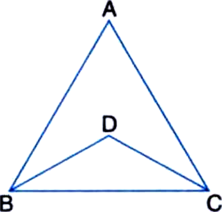
Solution not provided.
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that AD is also the median of the triangle.
Solution not provided.
ABC is a right angled triangle in which ∠A = 90° and AB = AC, find the values of ∠B and ∠C.
Solution not provided.
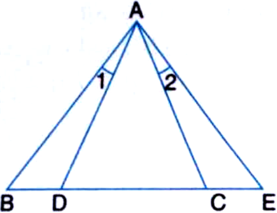
∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that:
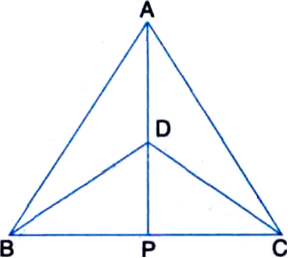
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Given: ∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. AD is extended to intersect BC at P.
To Prove: (i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Proof: (i) In ∆ABD and ∆ACD,
AB = AC ...(1)
| ∵ ∆ABC is an isosceles triangle
BD = CD ...(2)
| ∵ ADBC is an isosceles triangle
AD = AD ...(3) | Common
∴ ∆ABD ≅ ∆ACD | SSS Rule
(ii) In ∆ABP and ∆ACP,
AB = AC ...(4) | From(1)
∠ABP = ∠ACP ...(5)
| ∵ AB = AC From (1) ∴ ∠ABP = ∠ACP Angles opposite to equal sides of a triangle are
equal
∵ ∆ABD ≅ ∆ACD
| Proved in (i) above
∴ ∠BAP = ∠CAP ...(6) | C.P.C.T.
In view of (4), (5) and (6)
∆ABP ≅ ∆ACP | ASA Rule
(iii) ∵ ∆ABP ≅ ∆ACP
| Proved in (ii) above
∠BAP = ∠CAP | C.P.C.T.
⇒ AP bisects ∠A.
In ∆BDP and ∆CDP,
BD = CD ...(7) | From (2)
DP = DP ...(8) | Common
∵ ∆ABP ≅ ∆ACP
| Proved in (ii) above
∴ BP = CP ...(9) | C.P.C.T.
In view of (7), (8) and (9),
∆BDP ≅ ∆CDP | SSS Rule
∴ ∠BDP = ∠CDP | C.P.C.T.
⇒ DP bisects ∠D
⇒ AP bisects ∠D
(iv) ∵ ∆BDP ≅ ∆CDP
| Proved in (iii) above
∴ BP = CP ...(10) | C.P.C.T.
∠BPD = ∠CPD | C.P.C.T.
But ∠BPD + ∠CPD = 180°
| Linear Pair Axiom
∴ ∠BPD = ∠CPD = 90° ...(11)
In view of (10) and (11),
AP is the perpendicular bisector of BC.
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A.
Given: AD is an altitude of an isosceles triangle ABC in which AB = AC.
To Prove: (i) AD bisects BC
(ii) AD bisects ∠A.
Proof: (i) In right ∆ADB and right ∆ADC,
Hyp. AB = Hyp. AC | Given
Side AD = Side AD | Common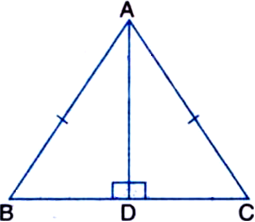
∴ ∆ADB ≅ ∆ADC | RHS Rule
∴ BD = CD | C.P.C.T.
⇒ AD bisects BC.
(ii) ∵ ∆ADB ≅ ∆ADC
| Proved in (i) above
∴ ∠BAD = ∠CAD | C.P.C.T.
⇒ AD bisects ∠A.
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of triangle PQR (see figure). Show that:
(i) ∆ABM ≅ ∆PQN
(ii) ∆ABC ≅ ∆PQR.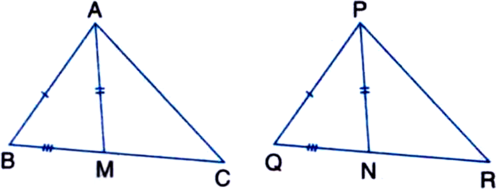
Given: Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆PQR.
To Prove: (i) ∆ABM ≅ ∆PQN
(ii) ∆ABC ≅ ∆PQR.
Proof: (i) In ∆ABM and ∆PQN,
AB = PQ ...(1) | Given
AM = PN ...(2) | Given
BC = QR
⇒ 2BM = 2QN
| ∵ M and N are the mid-points of BC and QR respectively
⇒ BM = QN ...(3)
In view of (1), (2) and (3),
∆ABM ≅ ∆PQN | SSS Rule
(ii) ∵ ∆ABM ≅ ∆PQN
| Proved in (1) above
∴ ∠ABM = ∠PQN | C.P.C.T.
⇒ ∠ABC = ∠PQR ...(4)
In ∆ABC and ∆PQR,
AB = PQ | Given
BC = QR | Given
∠ABC = ∠PQR | From (4)
∴ ∆ABC ≅ ∆PQR. | SAS Rule
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Given: BE and CF are two equal altitudes of a triangle ABC.
To Prove: ∆ABC is isosceles.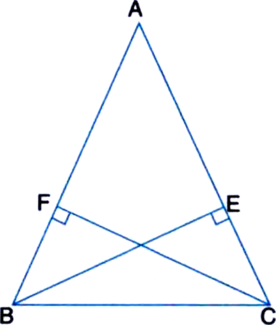
Proof: In right ∆BEC and right ∆CFB,
Side BE = Side CF | Given
Hyp. BC = Hyp. CB | Common
∴ ∆BEC ≅ ∆CFB | RHS Rule
∴ ∠BCE = ∠CBF | C.P.C.T.
∴ AB = AC
| Sides opposite to equal angles of a triangle are equal
∴ ∆ABC is isosceles.
ABC is an isosceles triangle with AB = AC. Draw AP π BC to show that ∠B = ∠C.
Given: ABC is an isosceles triangle with AB = AC.
To Prove: ∠B = ∠C
Construction: Draw AP π BC
Proof: In right triangle APB and right triangle
APC,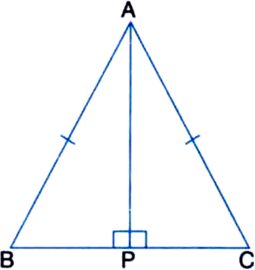
Hyp. AB = Hyp. AC | Given
Side AP = Side AP | Common
∴ ∆APB ≅ ∆APC | RHS Rule
∴ ∠ABP = ∠ACP | C.P.C.T.
⇒ ∠B = ∠C.
D is a point on side BC of ∆ABC such that AD = AC. Show that AB > AD.
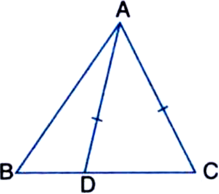
Solutuion not provided.
Prove that in a triangle the angle opposite to the longest side is greater than two-third of a right angle, i.e., greater than 60°.
Solutuion not provided.
In ∆ABC, if ∠A = 50° and ∠B = 60°, determine the shortest and the longest side of the triangle.
Solutuion not provided.
In a ∆DEF, if ∠D = 30°, ∠E = 60° then which side of the triangle is longest and which side is shortest?
Solutuion not provided.
In ∆ABC, ∠A = 60°, ∠B = 40°, which side of this triangle is the smallest? Give reasons for your answer.
Solutuion not provided.
In ∆PQR, ∠P = 100° and ∠R = 60°, which side of the triangle is the longest. Give reasons for your answer.
Solutuion not provided.
In the given figure, if AD is the bisector of ∠BAC then prove that
(i) AB > BD (ii) AC > CD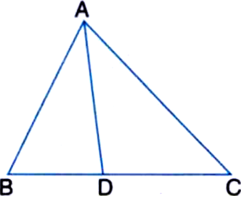
Solutuion not provided.
In the given figure, T is a point on the side QR of ∆PQR and S is a point such that TR = TS. Prove that PQ + PR > QS.

Solutuion not provided.
In the given figure, S is any point on the side QR of a ∆PQR. Show that PQ + QR + RP > 2PS.
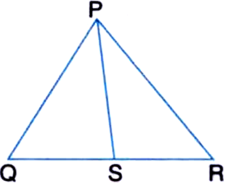
Solutuion not provided.
ABC is a triangle. Locate a point in the interior of ∆ABC which is equidistant from all the vertices of ∆ABC.
Sponsor Area
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
In a huge park, people are concentrated at three points (see figure):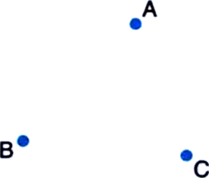
A: where there are different slides and swings for children,
B: near which a man-made lake is situated,
C: which is near to a large parking and exit. Where should an icecream parlour be set up so that maximum number of persons can approach it?
[Hint: The parlour should be equidistant from A, B and C.]
Complete the hexagonal and star shaped Rangolies [see figures (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
(i) (ii)
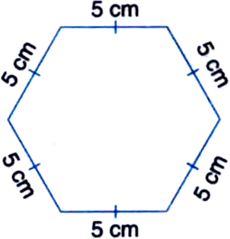
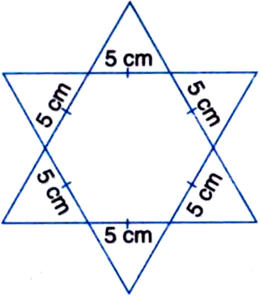
 (ii) Number of triangles = 24 × 12 = 288
(ii) Number of triangles = 24 × 12 = 288 Figure (ii) has more triangles.
Figure (ii) has more triangles.
If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent. This rule is known as
-
SAS congruence rule
-
ASA congruence rule
-
SSS congruence rule
-
RHS congruence rule.
D.
RHS congruence rule.
In ∆ABC, AB = AC and ∠ABD = ∠ACD, then ∆BCD is
-
equilateral
-
isosceles
-
equiangular
-
scalene
B.
isosceles
Which of the following is false?
-
The mid-point of the hypotenuse of a right triangle is equidistant from its vertices.
-
Each angle of an equilateral triangle is 60°.
-
The side opposite to the greater angle of a triangle is longer than the side opposite the smaller angle.
-
The two altitudes corresponding to two equal sides of a triangle are not equal.
D.
The two altitudes corresponding to two equal sides of a triangle are not equal.Sponsor Area
If ∆ABC ≅ ∆DEF by SSS congruence rule then:
-
AB = EF, BC = FD, CA = DE
-
AB = FD, BC = DE, CA = EF
-
AB = DE, BC = EF, CA = FD
-
AB = DE, BC = EF, ∠C = ∠F
C.
AB = DE, BC = EF, CA = FD
In ∆ABC, ∠B = 30°, ∠C = 80° and ∠A = 70° then,
-
AB > BC < AC
-
AB < BC > AC
-
AB > BC > AC
-
AB < BC < AC
D.
AB < BC < AC
In figure, which of the following statements is true?
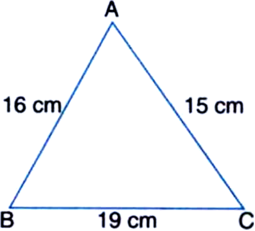
-
∠B = ∠C
-
∠B is the greatest angle in triangle
-
∠B is the smallest angle in triangle
-
∠A is the smallest angle in triangle
C.
∠B is the smallest angle in triangle
If ∆ABC is congruent to ∆DEF by SSS congruence rule, then:
-
∠C < ∠F
-
∠B < ∠E
-
∠A < ∠D
-
∠A = ∠D, ∠B = ∠E, ∠C = ∠F
D.
∠A = ∠D, ∠B = ∠E, ∠C = ∠F
If AB = QR, BC = PR and CA = PQ then
-
∆ABC ≅ ∆PQR
-
∆CBA ≅ ∆PRQ
-
∆BAC ≅ ∆RPQ
-
∆PQR ≅ ∆BCA
B.
∆CBA ≅ ∆PRQ
In the figure below, ABCD is a square and P is the mid point of AD. BP and CP are joined. Prove that ∠PCB = ∠PBC.
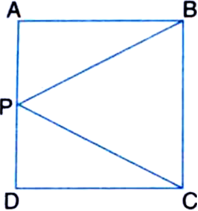
Solution not provided.
∆ABC is an isosceles triangle with AB = AC, D and E are the points on BC such that BE = CD. Prove that ∆ABD ≅ ∆ACE.

Solution not provided.
In the given figure, ABC is a triangle in which AB = AC and AD is an altitude on BC. Prove that AD bisects CA.
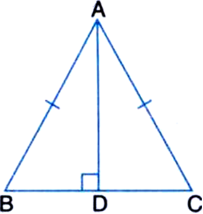
Solution not provided.
In the figure given below, PQR is a triangle and S is any point in its interior, show that SQ + SR < PQ + PR.
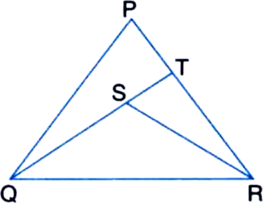

Solution not provided.
In the given figure, the diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.
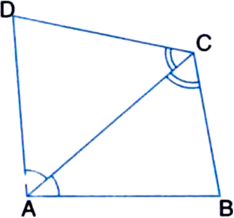
Solution not provided.
In the given figure, AB = CF, EF = BD and ∠AFE = ∠CBD. Prove that (i) ∆AFE ≅ ∆CBD and (ii) AE = CD
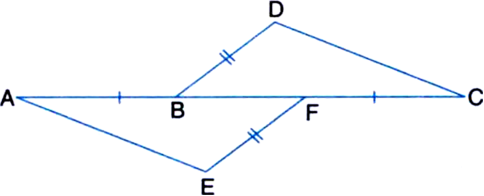
Solution not provided.
∆ABC is isosceles triangle in which AB = AC, P and Q are points on AB and AC such that AP = AQ. Prove that ∠ABQ = ∠ACP.
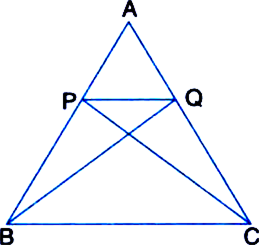
Solution not provided.
Q is a point on side SR of ∆PSR as shown in the figure below such that PQ = PR. Show that PS > PQ.
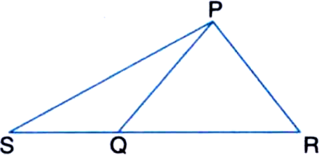
Solution not provided.
In figure, AB ⊥ AE, BC ⊥ AB, CE = DE and ∠AED = 120°. Find
(a) ∠EDC
(b) ∠DEC
(c) Hence prove that EDC is an equilateral triangle.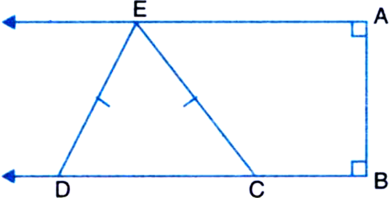
Solution not provided.
Mock Test Series
Sponsor Area
Sponsor Area