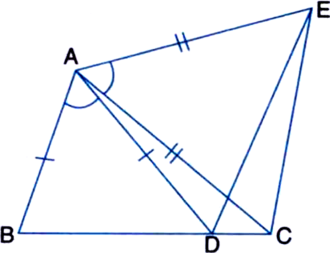
Areas Of Parallelograms And Triangles

Question

If the bisector of the vertical angle of a triangle bisects the base of the triangle, then prove that the triangle is isosceles.

Solution

Given: A ∆ABC in which the bisector of the vertical angle ∠BAC bisects the base BC, i.e., BD = CD

To Prove: ∆ABC is isosceles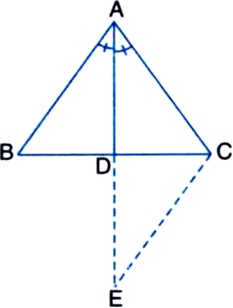

Construction: Produce AD to E such that AD = DE. Join EC.
Proof: In ∆ADB and ∆EDC,
BD = CD    | Given
AD = ED    | By construction
∠ADB = ∠EDC
| Vertically opposite angles
∴ ∆ADB ≅ ∆EDC
| SAS congruence rule ∴ AB = EC    ...(1) | CPCT
and    ∠BAD = ∠CED    | CPCT
But ∠BAD = ∠CAD    | Given
∴ ∠CAD = ∠CED
∴ AC = CE    ...(2)
| Sides opposite to equal angles of a triangle are equal
From (1) and (2),
AB = AC
∴ ∆ABC is isosceles.

Some More Questions From Areas of Parallelograms and Triangles Chapter

In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

For Daily Free Study Material Join wiredfaculty

Areas Of Parallelograms And Triangles

If the bisector of the vertical angle of a triangle bisects the base of the triangle, then prove that the triangle is isosceles.

Some More Questions From Areas of Parallelograms and Triangles Chapter

In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

Areas Of Parallelograms And Triangles

If the bisector of the vertical angle of a triangle bisects the base of the triangle, then prove that the triangle is isosceles.

Some More Questions From Areas of Parallelograms and Triangles Chapter

In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that. (i) ∆DAP ≅ ∆EBP(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:(i) ∆APX ≅ ∆BPY(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.