+91-8076753736 [email protected]

-->

Areas Of Parallelograms And Triangles

Question

Wired Faculty App

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

Solution

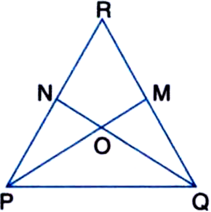
Given: ∠QPR = ∠PQR and M and N are respectively points on side QR and PR of ∆PQR, such that QM = PN.
To Prove: OP = OQ, where O is the point of intersection of PM and QN.
Proof: In ∆PNQ and ∆QMP,
PN = QM    | Given
PQ = QP    | Common
∠QPN = ∠PQM    | Given
∴ ∆PNQ ≅ ∆QMP
| SAS congruence rule
∴ ∠PNQ = ∠QMP    | CPCT
Again, in ∆PNO and ∆QMO,
PN = QM    | Given
∠PON = ∠QOM
| Vertically opposite angles
∠PNO = ∠QMO | Proved above
∴ ∆PNO ≅ ∆QMO
| AAS congruence rule
∴ OP = OQ    | CPCT

Some More Questions From Areas of Parallelograms and Triangles Chapter

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation