+91-8076753736 [email protected]

-->

Areas Of Parallelograms And Triangles

Question

Wired Faculty App

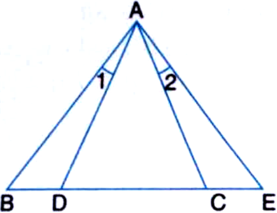
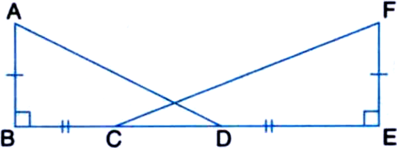
In figure, AB = BC, AD = EC. Prove that ∆ABE ≅ ∆CBD.

Solution

Given: AB = BC, AD = EC
To Prove: ∆ABE ≅ ∆CBD
Proof: In ∆ABC,
∵ AB = BC    | Given
∴ ∠BAC = ∠BCA    ...(1)
| Angles opposite to equal sides of a triangle are equal
AD = EC    | Given
⇒ AD + DE = EC + DE
⇒ AE = CD    ...(2)
Now, in ∆ABE and ∆CBD,
AE = CD    | From (2)
AB = CB    | Given
∠BAE = ∠BCD    | From (1)
∴ ∆ABE ≅ ∆CBD | SAS congruence rule.

Some More Questions From Areas of Parallelograms and Triangles Chapter

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.

In the given figure, if AB = FE, BC = ED, AB ⊥ BD and FE ⊥ EC, then prove that AD = FC.

In figure, OA = OB and OD = OC. Show that:
(i) ∆AOD ≅ ∆BOC and (ii) AD = BC.

AB is a line segment and line l is its perpendicular bisector. If a point P lies on I, show that P is equidistant from A and B.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation