+91-8076753736[email protected]
logo
logo
-->

Areas Of Parallelograms And Triangles

Question
CBSEENMA9002619
Wired Faculty App

BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

Solution

Given: BE and CF are two equal altitudes of a triangle ABC.
To Prove: ∆ABC is isosceles.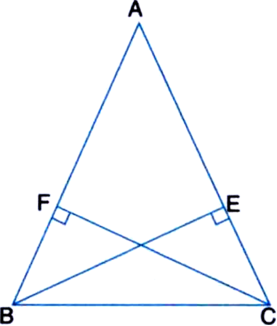

Proof: In right ∆BEC and right ∆CFB,
Side BE = Side CF    | Given
Hyp. BC = Hyp. CB    | Common
∴ ∆BEC ≅ ∆CFB    | RHS Rule
∴ ∠BCE = ∠CBF    | C.P.C.T.
∴ AB = AC
| Sides opposite to equal angles of a triangle are equal
∴ ∆ABC is isosceles.

Some More Questions From Areas of Parallelograms and Triangles Chapter

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i)    ∆APX ≅ ∆BPY
(ii)    AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.

In the given figure, if AB = FE, BC = ED, AB ⊥ BD and FE ⊥ EC, then prove that AD = FC.

In figure, OA = OB and OD = OC. Show that:
(i) ∆AOD ≅ ∆BOC and (ii) AD = BC.

AB is a line segment and line l is its perpendicular bisector. If a point P lies on I, show that P is equidistant from A and B.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation