+91-8076753736 [email protected]

-->

Areas Of Parallelograms And Triangles

Question

Wired Faculty App

In ∆ABC if AB = BC, then:

∠B > ∠C

∠A = ∠C

∠A = ∠B

∠A < ∠C

Solution

B.

∠A = ∠C

Some More Questions From Areas of Parallelograms and Triangles Chapter

ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see figure). Prove that:

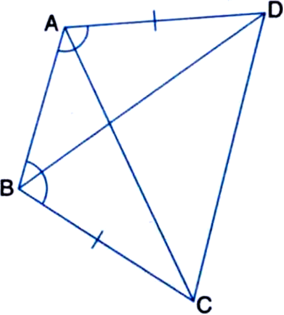
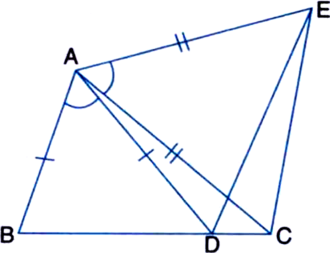
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.

I and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC ≅ ∆CDA.

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.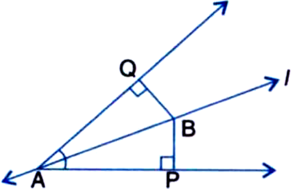

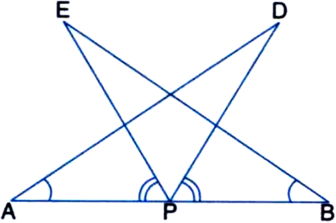
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation