+91-8076753736[email protected]
logo
logo
-->

Areas Of Parallelograms And Triangles

Question
CBSEENMA9002598
Wired Faculty App

In ∆ABC, AB = AC, ∠A = 36°. If the internal bisector of ∠C meets AB at D, Prove that AD = DC. 

Solution

Given: In ∆ABC, AB = AC, ∠A = 36°. The internal bisector of ∠C meets AB at D.
To Prove: AD = DC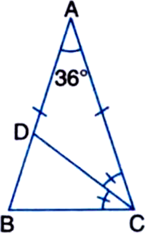

Proof: In ∆ABC,
∵ AB = AC
∴ ∠ABC = ∠ACB    ...(1)
| Angles opposite to equal sides of a triangle are equal
Also, ∠BAC + ∠ABC + ∠ACB = 180°
| Angle sum property of a triangle
⇒ 360° + ∠ABC + ∠ACB = 180°
⇒    ∠ABC + ∠ACB = 144° ...(2)
From (1) and (2),

angle A B C equals angle A C B equals 1 half cross times 144 degree equals 72 degree

Now, ∵ CD bisects ∠ACB

therefore space space space space angle BCD equals angle ACD equals 1 half cross times 72 degree equals 36 degree

Again, In ∆ACD,
∠ACD = ∠CAD (= 36°)
∴ AD = DC
| Sides opposite to equal angles of a triangle are equal

Some More Questions From Areas of Parallelograms and Triangles Chapter

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i)    ∆APX ≅ ∆BPY
(ii)    AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.

In the given figure, if AB = FE, BC = ED, AB ⊥ BD and FE ⊥ EC, then prove that AD = FC.

In figure, OA = OB and OD = OC. Show that:
(i) ∆AOD ≅ ∆BOC and (ii) AD = BC.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation