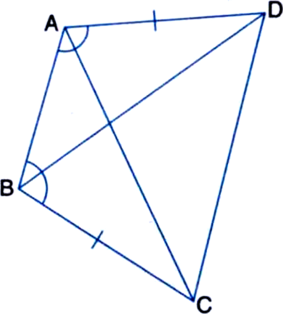
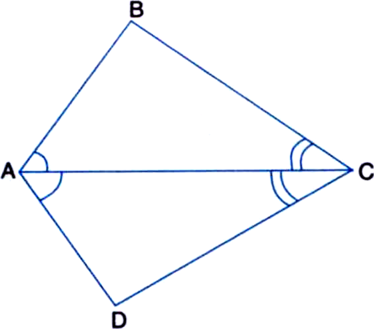
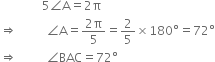+91-8076753736[email protected]
logo
logo
-->

Areas Of Parallelograms And Triangles

Question
CBSEENMA9002591
Wired Faculty App

ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that AD bisects ∠BAC and AB = CD. Prove that ∠BAC = 72°.
[Hint. Take a point P on AC such that BP bisects ∠B. Join P and D.]

Solution

Construction: Take a point P on AC such that BP bisects ∠B. Join P and D.
Proof: In ∆ABC,
∵ BP bisects ∠ABC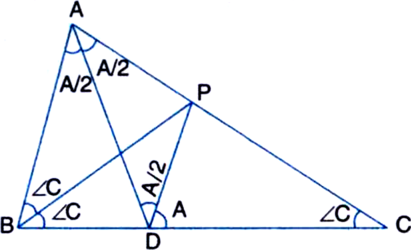

therefore space angle ABP equals angle PBC equals 1 half angle straight B equals 1 half left parenthesis 2 angle straight C right parenthesis equals angle straight C
In APBC,
∴ ∠PBC = ∠PCB (= ∠C)
∴ PB = PC    ...(2)
| Sides opposite to equal angles of∆PBC In ∆APB and ∆DPC,
AB = CD    | Given
PB = PC    | From (2)
∠ABP = ∠DCP (= ∠C)
∴ ∆APB ≅ ∆DPC    | SAS Axiom
∴ ∠BAP = ∠CDP (= ∠A)    ...(3)
| C.P.C.T.
and    AP = DP    ...(4) | C.P.C.T.
In ∆APD,
∵ AP = DP    | From (4)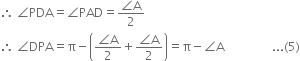
therefore space angle PDA equals angle PAD equals fraction numerator angle straight A over denominator 2 end fraction therefore space angle DPA equals straight pi minus open parentheses fraction numerator angle straight A over denominator 2 end fraction plus fraction numerator angle straight A over denominator 2 end fraction close parentheses equals straight pi minus angle straight A space space space space space space space space space space space space space space space space... left parenthesis 5 right parenthesis

Again from ∆DPC,
∠DPC = π - (∠A + ∠C)
∴ ∠DPA = π - ∠DPC = π - {π - (∠A + ∠C)} = ∠A + ∠C    ...(6)
From (5) and (6),
π - A = ∠A + ∠C ⇒ 2∠A + ∠C = π ...(7)
Again,
∠A + ∠B + ∠C = π
| ∵ The sum of three angles of ∆ABC = π ⇒ ∠A + 2∠C + ∠C = π | ∵ ∠B = 2∠C
⇒    ∠A + 3∠C = π    ...(8)
Multiplying (7) by 3, we get
6∠A + 3∠C = 3π    ...(9)
Subtracting (8) from (9), we get
         space space space space space space space space space space space space space space 5 angle straight A equals 2 straight pi rightwards double arrow space space space space space space space space space space angle straight A equals fraction numerator 2 straight pi over denominator 5 end fraction equals 2 over 5 cross times 180 degree equals 72 degree rightwards double arrow space space space space space space space space space space angle BAC equals 72 degree

Some More Questions From Areas of Parallelograms and Triangles Chapter

ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see figure). Prove that:

(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.

I and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC ≅ ∆CDA.

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

 

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation