+91-8076753736 [email protected]

-->

Areas Of Parallelograms And Triangles

Question

Wired Faculty App

In ∆ABC, if ∠A = 50° and ∠B = 60°, determine the shortest and the longest side of the triangle.

Solution

Solutuion not provided.

Some More Questions From Areas of Parallelograms and Triangles Chapter

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.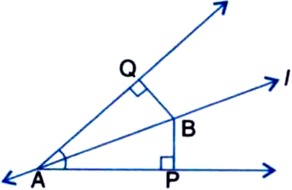

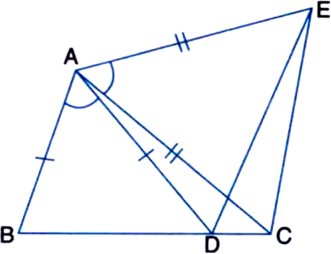
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

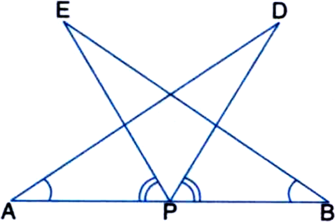
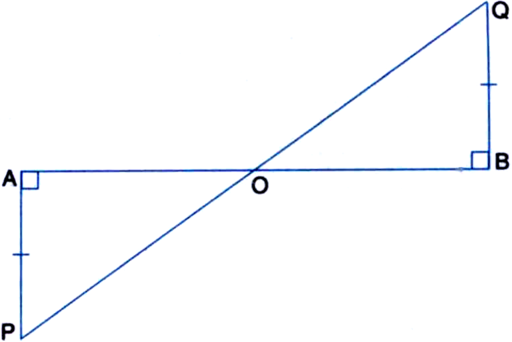
AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation