Question
In the given figure, if AD is the bisector of ∠BAC then prove that
(i) AB > BD (ii) AC > CD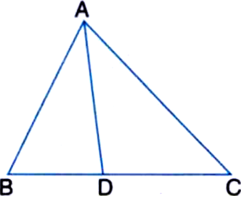
Solution
Solutuion not provided.
In the given figure, if AD is the bisector of ∠BAC then prove that
(i) AB > BD (ii) AC > CD
Solutuion not provided.
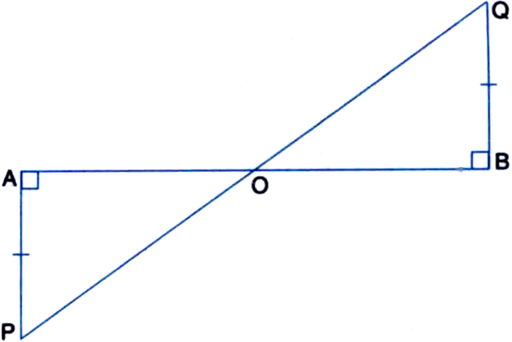
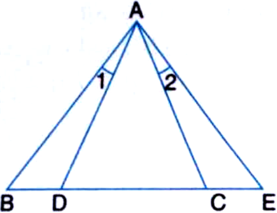
AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.
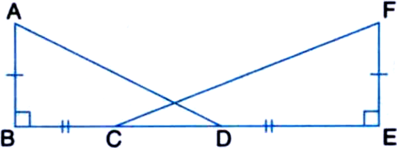
In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.
In figure, OA = OB and OD = OC. Show that:
(i) ∆AOD ≅ ∆BOC and (ii) AD = BC.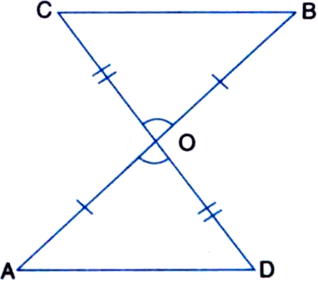
Mock Test Series