AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that

(i) AD bisects BC
(ii) AD bisects ∠A.

Solution

Given: AD is an altitude of an isosceles triangle ABC in which AB = AC.
To Prove: (i) AD bisects BC
(ii) AD bisects ∠A.
Proof: (i) In right ∆ADB and right ∆ADC,
Hyp. AB = Hyp. AC    | Given
Side AD = Side AD    | Common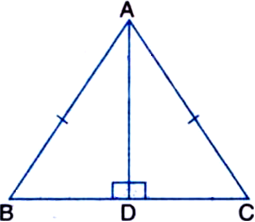

∴ ∆ADB ≅ ∆ADC    | RHS Rule
∴ BD = CD    | C.P.C.T.
⇒ AD bisects BC.
(ii) ∵ ∆ADB ≅ ∆ADC
| Proved in (i) above
∴ ∠BAD = ∠CAD    | C.P.C.T.
⇒ AD bisects ∠A.

Some More Questions From Areas of Parallelograms and Triangles Chapter

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

For Daily Free Study Material Join wiredfaculty

Areas Of Parallelograms And Triangles

AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that

(i) AD bisects BC
(ii) AD bisects ∠A.

Some More Questions From Areas of Parallelograms and Triangles Chapter

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.

In the given figure, if AB = FE, BC = ED, AB ⊥ BD and FE ⊥ EC, then prove that AD = FC.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

Areas Of Parallelograms And Triangles

AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that (i) AD bisects BC(ii) AD bisects ∠A.

Some More Questions From Areas of Parallelograms and Triangles Chapter

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:(i) ∆APX ≅ ∆BPY(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

In figure given below, AD is the median of ∆ABC.BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.

In the given figure, if AB = FE, BC = ED, AB ⊥ BD and FE ⊥ EC, then prove that AD = FC.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that

(i) AD bisects BC
(ii) AD bisects ∠A.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.