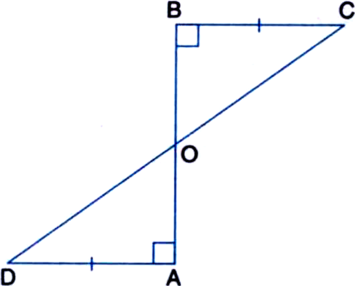
Areas Of Parallelograms And Triangles

Question

Suppose line segments AB and CD intersect at O in such a way that AO = OD and OB = OC. Prove that AC = BD but AC may not be parallel to BD.

Solution

In ∆OAC and ∆ODB,
OA = OD | Given
OB = OC | Given
∠AOC = ∠DOB
| Vertically Opposite Angles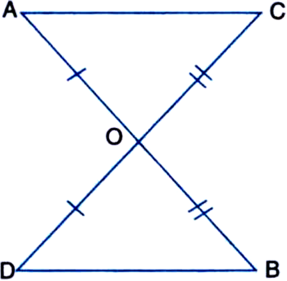

∴ ∆OAC ≅ ∆ODB    | SAS Axiom
∴ AC = BD    | C.P.C.T.
Also, ∠OAC = ∠ODB    | C.P.C.T.
and ∠OCA = ∠OBD    | C.P.C.T.
Thus ∠OAC may not be equal to ∠OBD and therefore, AC may not be parallel to BD
However, if OA = OC, then ∠OAC = ∠OCA
| Angles opposite to equal sides of ∆OAC But ∠OAC = ∠ODB
∴ ∠OCA = ∠ODB
But these angles form a pair of equal alternate angles
∴ AC || BD.

Some More Questions From Areas of Parallelograms and Triangles Chapter

AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.

I and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC ≅ ∆CDA.

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

For Daily Free Study Material Join wiredfaculty

Areas Of Parallelograms And Triangles

Suppose line segments AB and CD intersect at O in such a way that AO = OD and OB = OC. Prove that AC = BD but AC may not be parallel to BD.

Some More Questions From Areas of Parallelograms and Triangles Chapter

AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.

I and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC ≅ ∆CDA.

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

Areas Of Parallelograms And Triangles

Suppose line segments AB and CD intersect at O in such a way that AO = OD and OB = OC. Prove that AC = BD but AC may not be parallel to BD.

Some More Questions From Areas of Parallelograms and Triangles Chapter

AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.

I and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC ≅ ∆CDA.

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:(i) ∆APB ≅ ∆AQB(ii) BP = BQ or B is equidistant from the arms of ∠A.

In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that. (i) ∆DAP ≅ ∆EBP(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:(i) ∆APX ≅ ∆BPY(ii) AB and XY bisect each other at P.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.