Areas Of Parallelograms And Triangles

Question

In the given figure, AE bisects ∠DAC and ∠B = ∠C, prove that AE || BC.

Solution

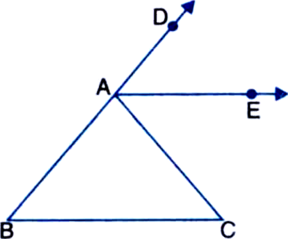
Given: AE bisects ∠DAC and ∠B = ∠C
To Prove: AE || BC
Proof: In ∆ABC,
Ext. ∠DAC = ∠ABC + ∠ACB ...(1)
| An exterior angle of a triangle is equal to the sum of its two interior opposite angles
⇒ ∠DAC = ∠ACB + ∠ACB
| ∵ ∠B = ∠C (Given)
⇒ ∠DAC = 2∠ACB
⇒ 2∠CAE = 2∠ACB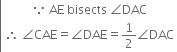
$left enclose table row cell because space AE space bisects space angle DAC end cell row cell therefore space angle CAE equals angle DAE equals 1 half angle DAC end cell end table end enclose$
⇒ ∠CAE = ∠ACB
But these angles form a pair of equal alternate interior angles
∴ AE || BC

Some More Questions From Areas of Parallelograms and Triangles Chapter

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

For Daily Free Study Material Join wiredfaculty

Areas Of Parallelograms And Triangles

In the given figure, AE bisects ∠DAC and ∠B = ∠C, prove that AE || BC.

Some More Questions From Areas of Parallelograms and Triangles Chapter

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

Areas Of Parallelograms And Triangles

In the given figure, AE bisects ∠DAC and ∠B = ∠C, prove that AE || BC.

Some More Questions From Areas of Parallelograms and Triangles Chapter

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:(i) ∆APB ≅ ∆AQB(ii) BP = BQ or B is equidistant from the arms of ∠A.

In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that. (i) ∆DAP ≅ ∆EBP(ii) AD = BE.

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:(i) ∆APX ≅ ∆BPY(ii) AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.