+91-8076753736[email protected]
logo
logo
-->

Areas Of Parallelograms And Triangles

Question
CBSEENMA9002597
Wired Faculty App

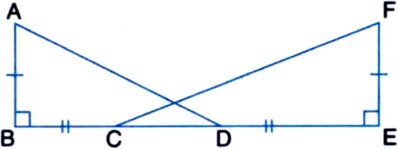
 In figure, ABCD is a square and ∠DEC is an equilateral triangle. Prove that

(i)     ∆ADE ≅ ∆BCE
(ii)    AE = BE
(iii)   ∠DAE = 15°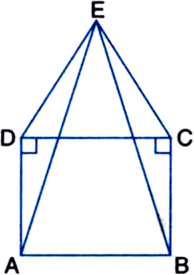

Solution

Given: ABCD is a square and ∆DEC is an equilateral triangle.

To Prove:

(i)    ∆ADE ≅ ∆BCE

(ii)    AE = BE

(iii)    ∠DAE = 15°

Proof: (i) In ∆ADE and ∆BCE,
   AD = BC
           left enclose table row cell because space ABCD thin space is space straight a space square end cell row cell therefore AB equals BC equals CD equals DA end cell end table end enclose
  DE=CE
    
          left enclose table row cell because space increment EDC space is space equilateral end cell row cell therefore space ED space equals space DC space equals space CE end cell end table end enclose
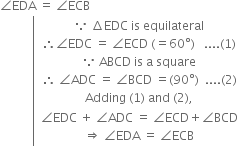
 angle EDA space equals space angle ECB space space space space space space space space space space space left enclose table row cell because space increment EDC space is space equilateral end cell row cell therefore angle EDC space equals space angle ECD space left parenthesis equals 60 degree right parenthesis space space space.... left parenthesis 1 right parenthesis end cell row cell because space ABCD space is space straight a space square end cell row cell therefore space angle ADC space equals space angle BCD space equals left parenthesis 90 degree right parenthesis space space.... left parenthesis 2 right parenthesis end cell row cell Adding space left parenthesis 1 right parenthesis space and space left parenthesis 2 right parenthesis comma end cell row cell table row cell angle EDC space plus space angle ADC space equals space angle ECD plus angle BCD end cell row cell rightwards double arrow space angle EDA space equals space angle ECB end cell end table end cell end table end enclose

∴ ∆ADE ≅ ∆BCE | SAS congruence rule
(ii)    ∵ ∆ADE ≅ ∆BCE | Proved in (1)
∴ AE = BE    | CPCT
(iii)    In ∆DAE,
∵ DE = DA    | Given
∴ ∠DAE = ∠DEA    ...(1)
| Angles opposite to equal sides of a triangle are equal Also, ∠ADE + ∠DAE + ∠DEA = 180°
| Angle sum property of a triangle
⇒ (∠ADC + ∠EDC) + ∠DAE + ∠DEA = 180°
⇒ (90° + 60°) + ∠DAE + ∠DEA = 180°
⇒ ∠DAE + ∠DEA = 30°    ...(2)
From (1) and (2),
∠DAE = 15° = ∠DEA

Some More Questions From Areas of Parallelograms and Triangles Chapter

In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.

In figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.

AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i)    ∆APX ≅ ∆BPY
(ii)    AB and XY bisect each other at P.

In figure, ∠QPR = ∠PQR and M and N are respectively points on sides QR and PR of ∆PQR, such that QM = PN. Prove that OP = OQ, where O is the point of intersecting of PM and QN.

In figure, ∠B = ∠.E, BD = CE and ∠1 = ∠2. Show ∆ABC ≅ ∆AED.

In figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.

In the given figure, if AB = FE, BC = ED, AB ⊥ BD and FE ⊥ EC, then prove that AD = FC.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation