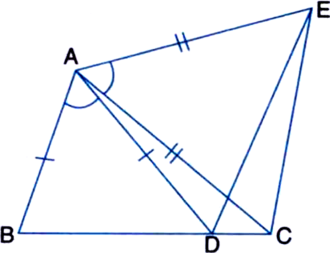
Given: PS = PR, ∠TPS = ∠QPR
To Prove: PT = PQ
Proof: In ∆PSR,
∵ PS = PR | Given
∴ ∠PSR = ∠PRS ...(1)
| Angles opposite to equal sides of a triangle are equal
⇒ ∠TPS + ∠PTS = ∠QPR + ∠PQR
| An exterior angle of a triangle is equal to the sum of its two interior opposite angles
⇒ ∠PTS = ∠PQR | Using (1)
⇒ ∠PTQ = ∠PQT ∴ PT = PQ
| Sides opposite to equal angles of a triangle are equal.
Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.
AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i) ∆APX ≅ ∆BPY
(ii) AB and XY bisect each other at P.
Mock Test Series
