Mathematics Chapter 6 Lines And Angles
Sponsor Area
NCERT Solution For Class 9 About 2.html
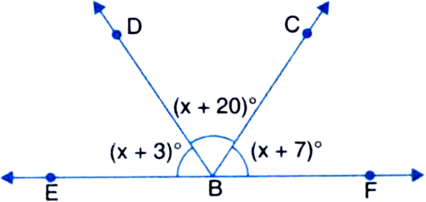
Ray OE bisects ∠AOB and OF is the ray opposite to OE. Show that ∠FOB = ∠FOA.
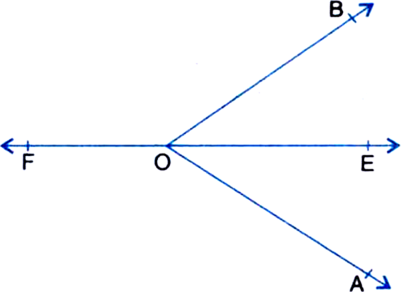
∠FOB + ∠BOE = 180° ...(1)
| Linear Pair Axiom
∠FOA + ∠AOE = 180° ...(2)
| Linear Pair Axiom
From (1) and (2),
∠FOB + ∠BOE = ∠FOA + ∠AOE ...(3)
But ∠BOE = ∠AOE
| ∵ Ray OE bisects ∠AOB
∴ From (3),
⇒ ∠FOB = ∠FOA.
Rays OA, OB. OC, OD and OE have the common initial point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.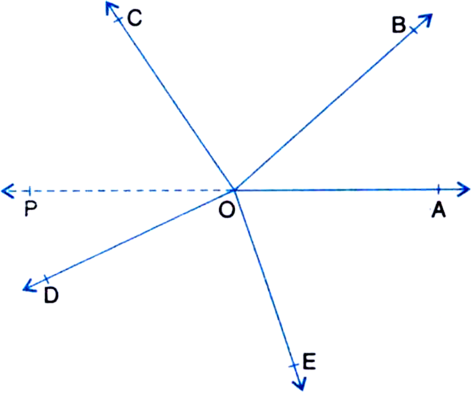
Construction. Draw a ray OP opposite to ray OA.
Proof. ∠AOB + ∠BOC + ∠COP = 180° ...(1)
| ∵ A straight angle = 180°
∠POD + ∠DOE + ∠EOA = 180° ...(2)
| ∵ A straight angle = 180°
Adding (1) and (2), we get
∠AOB + ∠BOC + (∠COP + ∠POD) + ∠DOE + ∠EOA = 180° + 180° = 360°
⇒ ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.
Prove “if two lines intersect each other, then the vertically opposite angles are equal.”
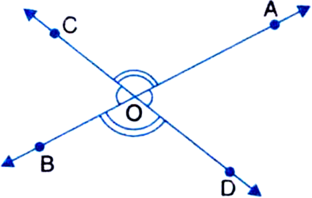
This leads to two pairs of vertically opposite angles, namely,
(i) ∠AOC and ∠BOD
(ii) ∠AOD and ∠BOC
We are to prove that
(i) ∠AOC = ∠BOD
and (ii) ∠AOD = ∠BOC
∵ Ray OA stands on line CD Therefore,
∠AOC + ∠AOD = 180° ...(1)
| Linear Pair Axiom
∵ Ray OD stands on line AB Therefore,
∠AOD + ∠BOD = 180° ...(2)
| Linear Pair Axiom
From (1) and (2),
∠AOC + ∠AOD = ∠AOD + ∠BOD
⇒ ∠AOC = ∠BOD
Similarly, we can prove that
∠AOD = ∠BOC
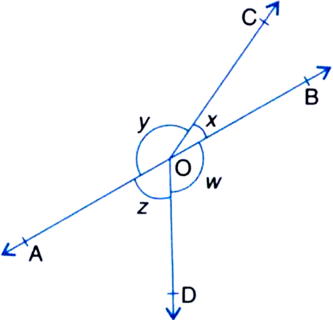
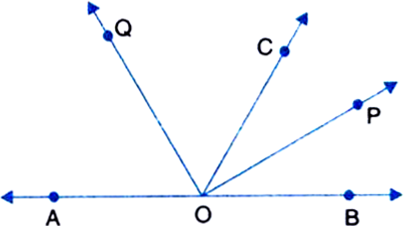
In figure, OP bisects ∠AOC, OQ bisects ∠BOC and OP ⊥ OQ. Show that the points A, O and B are collinear.

Given: OP bisects ∠AOC, OQ bisects ∠BOC and OP ⊥ OQ.
To Prove: The points A, O and B are collinear.
Proof: ∵ OP bisects ∠AOC
∴ ∠AOP = ∠COP ...(1)
∵ OQ bisects ∠BOC
∠BOQ = ∠COQ ...(2)
Now, ∠AOB
= ∠AOP + ∠COP + ∠COQ + ∠BOQ
= ∠COP + ∠COP + ∠COQ + ∠COQ
| From (1) and (2)
= 2(∠COP + ∠COQ)
= 2 ∠POQ
= 2(90°) | ∵ OP ⊥ OQ
= 180°
∴ The points A, O and B are collinear.
| By converse of Linear Pair Axiom
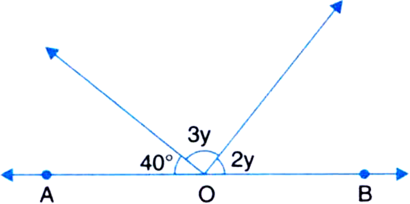
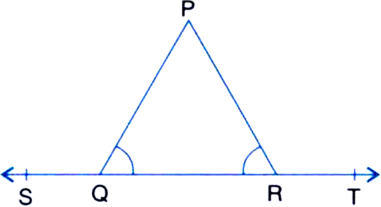
In figure, if y = 20°, prove that the line AOB is a straight line.


∵ Sum of all the angle round a point is equal to 360°.
∴ y + (3x - 15) + (y + 5) + 2y + (4y + 10) + x = 360°
⇒ 4x + 8y = 360°
⇒ x + 2y = 90°
⇒ x + 2(20°) = 90°
⇒ x + 40° = 90°
⇒ x = 50°
Now, y + 3x - 15 + y + 5 = 3x + 2y - 10
= 3(50°) + 2(20°) - 10
= 150° + 40° - 10°
= 180°
∴ AOB is a straight line.
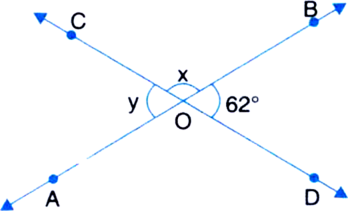
In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex angle EOC.

∵ BOA is a line
(∠AOC + ∠BOE) + ∠EOC = 180°
⇒ 70° + EOC = 180°
⇒ ∠EOC = 110°
⇒ Reflex ∠EOC = 360° - 110° = 250°
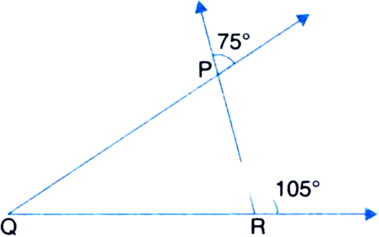
In figure, lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ = 5 : 7, find all the angles.

Solution not provided.
Ans. ∠POR = 75°, ∠ROQ = 105°, ∠POS = 105°, ∠SOQ = 75°
In figure, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ, respectively. If ∠POS = x, find ∠ROT.
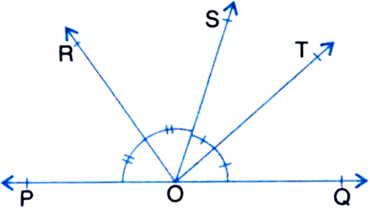
Solution not provided.
Ans. 90°
If the complement of an angle is one-third of its supplement, find the angle.
Solution not provided.
Ans. 45°
In figure, if ∠POR and ∠QOR form a linear pair and a - b = 80° then find the value of a and b.

Solution not provided.
Ans. 130°, 50°
What value of x would make XOY a line if ∠XOZ = 7x + 20° and ∠YOZ = 3x in figure.
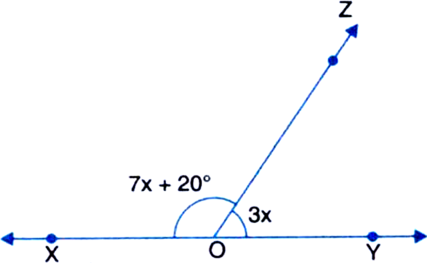
Solution not provided.
Ans. 16
Two supplementary angles are in the ratio 4 : 5. Find the angles.
Solution not provided.
Ans. 80°, 100°
In figure, lines AB and CD intersect at O. If ∠AOD : ∠DOC = 4 : 5 then find ∠COB.

Solution not provided.
Ans. 80°
An angle is equal to five times of its complement. Find the measure of the angle.
Solution not provided.
Ans. 75°
In figure, lines I and m intersect each other at O. If x = 40°, then, find the values of y, z and w.

Solution not provided.
Ans. 140°, 40°, 140°,
Sponsor Area
If OA, OB. OC and OD are the rays such that ∠AOB = ∠COD = 150°, ∠BOC = 30° and ∠AOD = 30°. Is it true that AOC and BOD are straight lines? Justify your answer.

Solution not provided.
Ans. Yes
In figure, angles x and y are supplementary angles. If ∠x = 110°, find the value of y.
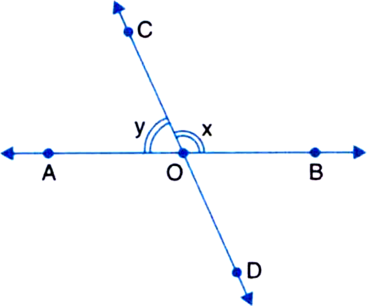
Solution not provided.
Ans. 70°
In figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
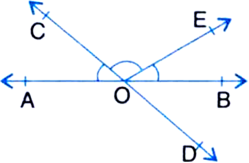
∵ Lines AB and CD intersect at O
∴ ∠AOC = ∠BOD
| Vertically Opposite Angles
But ∠BOD = 40° ...(1) | Given
∴ ∠AOC = 40° ...(2)
Now, ∠AOC + ∠BOE = 70°
⇒ 40° + ∠BOE = 70° | Using (2)
⇒ ∠BOE = 70° - 40°
⇒ ∠BOE = 30°
Again,
Reflex ∠COE
= ∠COD + ∠BOD + ∠BOE
= ∠COD + 40° + 30°
| Using (1) and (2)
= 180° + 40° + 30°
| ∵ Ray OA stands on line CD
|∴ ∠AOC + ∠AOD = 180° (Linear Pair Axiom) ⇒ ∠COD = 180°
= 250°.
In figure, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.
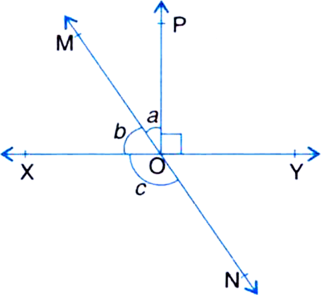
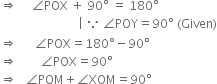
a : 2 = 2 : 3
b = 3k
Putting the values of a and b in (1), we get
2k + 3k = 900
∵ Ray OX stands on line MN
∴ ∠XOM + ∠XON = 180°
| Linear Pair Axiom
⇒ b + c = 180°
⇒ 54° + c = 180° | Using (2)
⇒ c = 180° - 54°
⇒ c = 126°.
In figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
∵ Ray QP stands on line ST
∴ ∠PQS + ∠PQR = 180° ...(1)
| Linear Pair Axiom
∵ Ray RP stands on line ST
∴ ∠PRQ + ∠PRT = 180° ...(2)
| Linear Pair Axiom
From (1) and (2), we obtain
∠PQS + ∠PQR = ∠PRQ + ∠PRT
⇒ ∠PQS = ∠PRT.
| ∵ ∠PQR = ∠PRQ (Given)
In figure, if x + y = w + z, then prove that AOB is a line.
x + y = w + z ...(1) | Given
∵ The sum of all the angles round a point is equal to 360°.![]() x + y + w + z = 3600
x + y + w + z = 3600 ![]() x + y + x + y = 3600 | Using (1)
x + y + x + y = 3600 | Using (1)![]() 2(x + y) = 3600
2(x + y) = 3600![]()
![]() x + y = 1800
x + y = 1800
∴ AOB is a line.
| If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.
In figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that

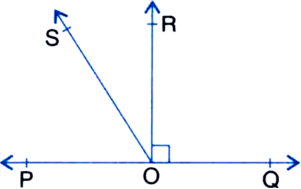
∵ Ray OR is perpendicular to line PQ.
∴ ∠QOR = ∠POR = 90° ...(1)
∠QOS = ∠QOR + ∠ROS ...(2)
∠POS = ∠POR - ∠ROS ...(3)
From (2) and (3),
∴ ∠QOS - ∠POS = (∠QOR - ∠POR) + 2∠ROS = 2∠ROS | Using (1)![]()
It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
∵ Ray YZ stands on line PX
∴ ∠XYZ+ ∠ZYP = 180°
| Linear Pair Axiom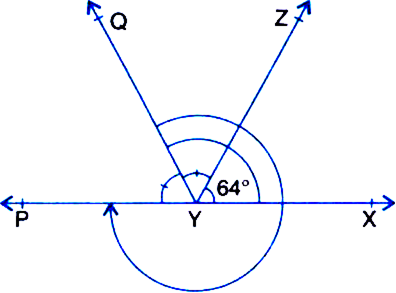
⇒ 64° + ∠ZYP = 180°
| ∵ ∠XYZ = 64° (Given)
⇒ ∠ZYP = 180° - 64°
⇒ ∠ZYP = 116° ...(1)![]() Ray YQ bisects
Ray YQ bisects ![]()
![]()
| Using (1)
= 580 ...(2)
![]()
![]() The sum of all the angles round apoint is equal to 3600
The sum of all the angles round apoint is equal to 3600
Again, ![]()
= 640 + 580![]() (Given) and
(Given) and ![]()
[ From (2) ]
= 1220.
In figure, if AOB is a line, OP bisects ∠BOC and OQ bisects ∠AOC, show that ∠POQ is a right angle.
In the given figure, lines XY and MN intersect each other at O. If ∠POY = 90° and a : b = 2 : 3, then find c.
∵ XOY is a line
∴ b + a + 90° = 180°
![]() a + b = 900
a + b = 900
2 + 3 = 5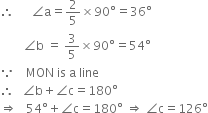
In figure, find the values of x and y and then show that AB || CD.
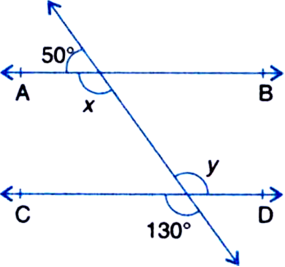
∵ Ray AE stands on line GH ∴AEG + ∠AEH = 180°
| Linear Pair Axiom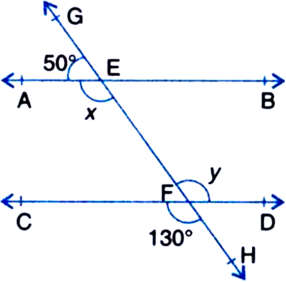
⇒ 50° + x = 180°
⇒ x = 180° - 50° = 130° ...(1)
y = 130° ...(2)
| Vertically Opposite Angles
From (1) and (2), we conclude that
x = y
But these are alternate interior angles and they are equal.
So, we can say that AB || CD.
In figure, if AB || CD, CD || EF and y : z = 3 : 7, find x.
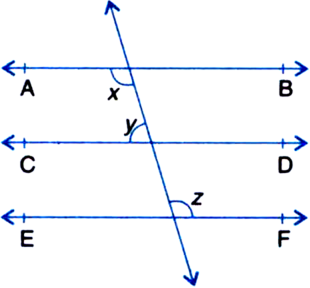
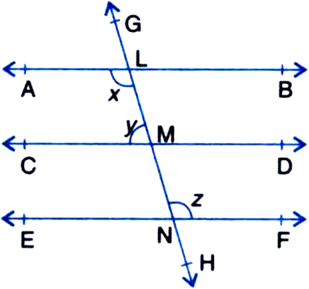
∵ AB || CD
and CD || EF
∴ AB || EF
| Lines parallel to the same line are parallel to each other
∴ x = z ...(1)
| Alternate Interior Angles
x + y = 180° ...(2)
| Consecutive interior angles on the same side of the transversal GH to parallel lines AB and CD
From (1) and (2),
z + y = 180°
y : z = 3 : 7
Sum of the ratios = 3 + 7 = 10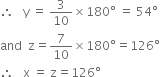
In figure, if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
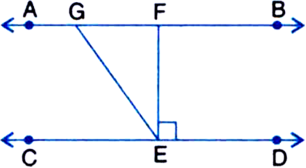
(i) ∠AGE = ∠GED = 126°
| Alternate Interior Angles
(ii) ∠GED = 126°
⇒ ∠GEF + ∠FED = 126°
⇒ ∠GEF + 90° = 126°
| ∵ EF ⊥ CD ∴ ∠FED = 90°
⇒ ∠GEF = 126° - 90° = 36°
(iii) ∠GEC + ∠GEF + ∠FED = 180°
| ∵ CD is a line
⇒ ∠GEC + 36° + 90° = 180°
⇒ ∠GEC + 126°= 180°
⇒ ∠GEC = 180° - 126° = 54°
Now, ∠FGE = ∠GEC = 54°
| Alternate Interior Angles
In figure, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
[Hint. Draw a line parallel to ST through point R.]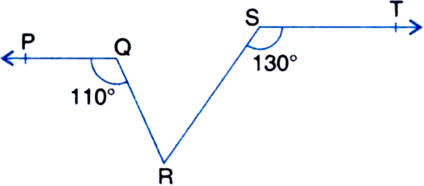
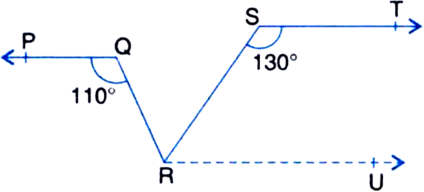
∠RST + ∠SRU = 180°
| Sum of the consecutive interior angles on the same side of the transversal is 180°
⇒ 130° + ∠SRU = 180°
⇒ ∠SRU = 180° - 130° = 50° ...(1)
∠QRU = ∠PQR = 110°
| Alternate Interior Angles
⇒ ∠QRS + ∠SRU = 110°
⇒ ∠QRS + 50° = 110° | Using (1)
⇒ ∠QRS = 110° - 50° = 60°.
In figure, if AB II CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.
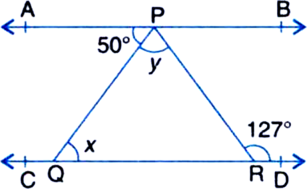
x = ∠APQ = 50°
| Alternate Interior Angles
∠APQ + y = ∠PRD = 127°
| Alternate Interior Angles
50° + y = 127°
y = 127° - 50° = 77°
In figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
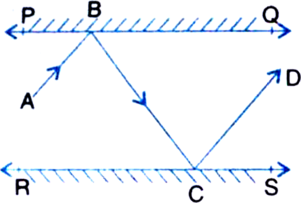
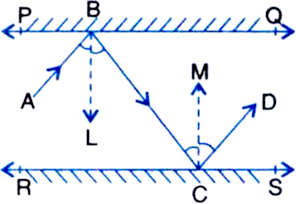
Proof: ∵ BL ⊥ PQ, CM ⊥ RS and PQ || RS ∴ BL || CM
∠LBC = ∠MCB ...(1)
| Alternate Interior Angles
∠ABL = ∠LBC ...(2)
| ∵ Angle of incidence = Angle of reflection
∠MCB = ∠MCD ...(3)
| ∵ Angle of incidence = Angle of reflection
From (1), (2) and (3), we get
∠ABL = ∠MCD ...(4)
Adding (1) and (4), we get
∠LBC + ∠ABL = ∠MCB + ∠MCD
⇒ ∠ABC = ∠BCD
But these are alternate interior angles and they are equal.
So, AB || CD.
In figure, if x = y and a = b, prove that r || n.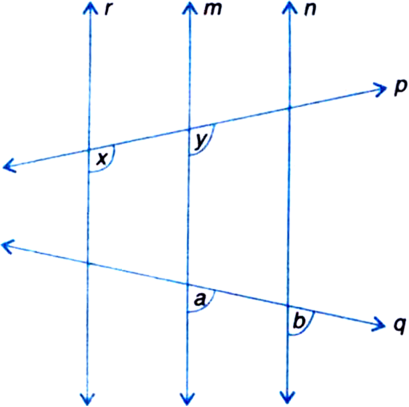
r and m are two lines and a transversal p intersects them such that
x = y
But these angles form a pair of equal corresponding angles
∴ r || m ...(1)
Again, m and n are two lines and a transversal q intersects them such that
a = b
But these angles form a pair of equal corresponding angles
∴ m || n ...(2)
From (1) and (2), we have r || n.
If two lines are perpendicular to the same line, prove that they are parallel to each other.
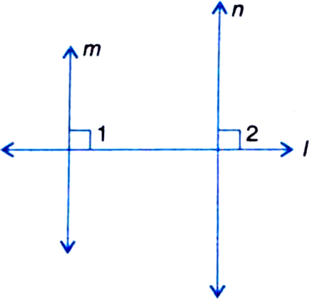
Then,
∠1 = 90°
∠2 = 90°
∴ ∠1 = ∠2
But these angles form a pair of equal corresponding angles
∴ m || n
In figure, EF is a transversal to two parallel lines AB and CD, GM and HL are the bisectors of the corresponding angles EGB and EHD. Prove that GM || HL.
[Hint. First prove that ∠EGM = ∠GHL]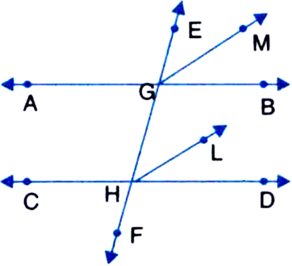
AB || CD and a transversal EF intersects them
∴ ∠EGB = ∠GHD
| Corresponding Angles
⇒ 2 ∠EGM = 2 ∠GHL
| ∵ GM and HL are the bisectors of ∠EGB and ∠EHD respectively.
⇒ ∠EGM = ∠GHL
But these angles form a pair of equal corresponding angles for lines GM and HL and transversal EF.
∴ GM || HL.
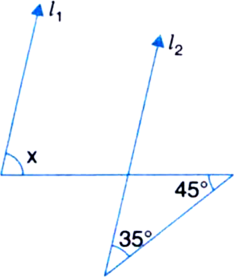
In figure, if AB || CD then find the value of y.
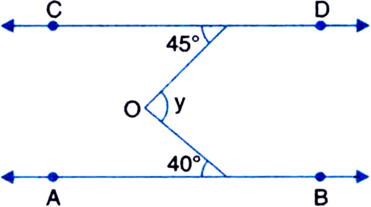
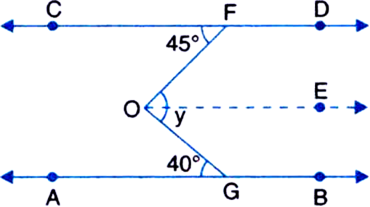
Construction: Through O draw OE || AB || CD
Now, y = ∠FOG
= ∠FOE + ∠GOE
= ∠CFO + ∠AGO
∠FOE = ∠CFO
(Alternate Interior Angles)
∠GOE = ∠AGO (Alternate Interior Angles)
= 45° + 40°
= 85°
In figure, is line I parallel to m? Justify your answer.
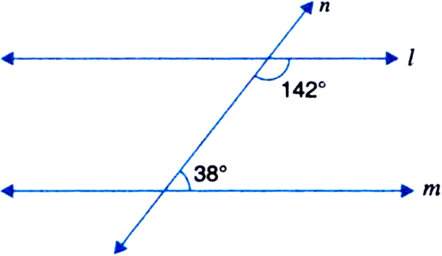
We see that
142° + 38° = 180°, i.e., the sum of the consecutive interior angles on the same side of
the transversal m is 180°.
So, by converse of consecutive interior angles axiom,
l || m
In figure, PQ || RS and T is any point as shown in the figure then show that
∠PQT + ∠QTS + ∠RST = 360°.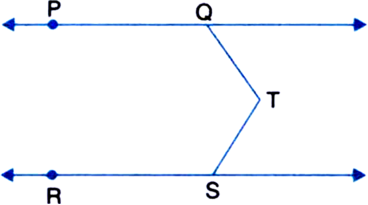
Given: PQ || RS and T is any point.
To Prove: ∠PQT + ∠QTS + ∠RST = 360°
Construction: Through T, draw TU || PQ || RS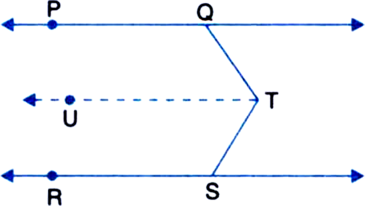
Proof: ∵ PQ || UT | By construction and a transversal QT intersects then
∴ ∠PQT + ∠QTU = 180° ...(1)
| Sum of consecutive interior angles on the same sides of a transversal is 180°
∵ UT || RS | By construction and a transversal TS intersects them
∴ ∠UTS + ∠RST = 180° ...(2)
| Sum of consecutive interior angles on the same side of a transversal is 180°
Adding (1) and (2), we get
∠PQT + (∠QTU + ∠UTS) + ∠RST = 360°
⇒ ∠PQT + ∠QTS + ∠RST = 360°
Sponsor Area
If l, m, n are three lines such that l || m and n ⊥ l, then prove that n ⊥ m.
Given: l, m, n are three lines such that l || m and n ⊥ l.
To Prove: n ⊥ m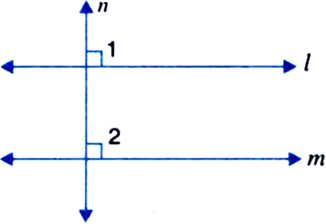
Proof: ∵ l || m and n is a transversal
∵ ∠1 = ∠2 | Corresponding angles
But ∠1 = 90° | ∵ n ⊥ l (given)
∴ ∠2 = 90°
⇒ n ⊥ m
In figure, l || m, show that ∠1 + ∠2 - ∠3 = 180°.
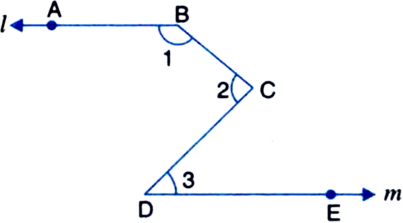
Given: l || m
To Prove: ∠1 + ∠2 - ∠3 = 180°
Construction: Through C, draw CF || l || m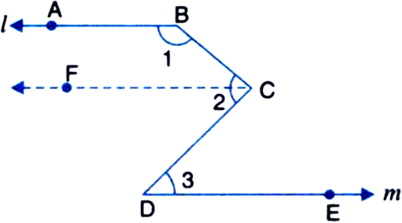
Proof: ∵ l || CF by construction and a transversal BC intersects them
∴ ∠1 + ∠FCB = 180°
| ∵ Sum of consecutive interior angles on the same side of a transversal is 180°
⇒ ∠1 + ∠2 - ∠FCD = 180° ...(1)
But ∠FCD = ∠3 ...(2)
| Alternate interior angles
∴ From (1) and (2),
∠1 + ∠2 - ∠3 = 180°
In figure, AB || CD and CD || EF. Also EA ⊥ AB. If ∠BEF = 40°, then find x, y, z.
∵ CD || EF and a transversal DE intersects them
∴ y + 40° = 180°
| Sum of consecutive interior on the same side of a transversal is 180°
⇒ y = 180° - 40° = 140°
∵ AB || CD and a transversal BD intersects them
x = y | Corresponding angles
⇒ x = 140°
∵ EA ⊥ AB and AB || EF
∵ EA ⊥ EF
| If a line is perpendicular to a line, then it is perpendicular to the parallel line also
⇒ ∠AEF = 90°
⇒ z + 40° = 90°
⇒ z = 50°
In the figure below, l1 || l2 and a1 || a2. Find the value of x.
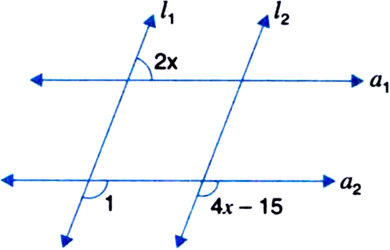
∠1 = 4x - 15 | Corresponding angles
2x = ∠1 = 4x - 15
| Corresponding angles![]()
Two parallel lines are intersected by a transversal. Then, prove that the bisectors of two pairs of interior angles enclose a rectangle.
Given: Two parallel lines AB and CD are intersected by a transversal EF in points G and H respectively. The bisectors of two pairs of interior angles intersect in L and M.
To Prove: GLHM is a rectangle.
Proof: ∵ AB || CD and a transversal EF intersects them![]()
| Alternate interior angles![]()
| Halves of equals are equal![]()
But these form a pair of equal alternate interior angles
∴ GM || HL ...(1)
Similarly, we can show that
HM || GL ...(2)
In view of (1) and (2),
GLHM is a parallelogram
| A quadrilateral is a parallelogram if its both the pairs of opposite sides are parallel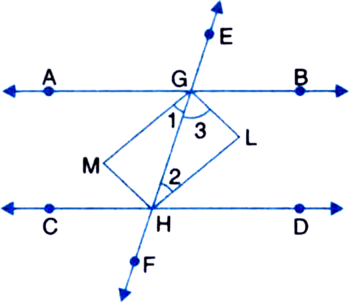
Now, since the sum the consecutive interior angles on the same side of a transversal is 180°
| Halves of equals are equal
⇒ ∠3 + ∠2 = 90° ...(3)
In ∆GHL,
∠3 + ∠2 + ∠GLH = 180°
| Angle sum property of a triangle
⇒ 90° + ∠GLH = 180°
| From (3)
∠GLH = 90°
⇒ GLHM is a rectangle
| A parallelogram with one of its angles of measure 90° is a rectangle.
In the figure, if PQ || RS, ∠MXQ = 135° and ∠MYR = 40°, find ∠XMY.
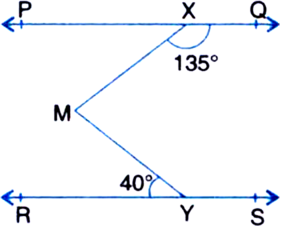
Solution not provided.
Ans. 850
In the figure, AB || CD and CD || EF. Also EA ⊥ AB. If ∠BEF = 55°, find the values of x, y and z.
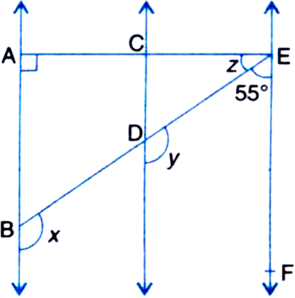
Solution not provided.
Ans. x = y = 125°, z = 35°.
AB and CD are the bisectors of the two alternate interior angles formed by the intersection of a transversal 't' with parallel lines l and m. Show that AB || CD.
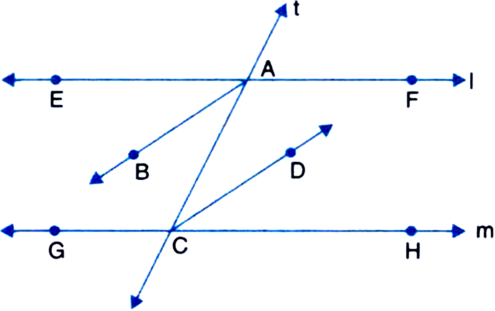
Solution not provided.
Ans. 125°, 125°, 35°
In figure, l || m. ∠1 and ∠2 are in the ratio 5 : 4. Find ∠3 and ∠4.
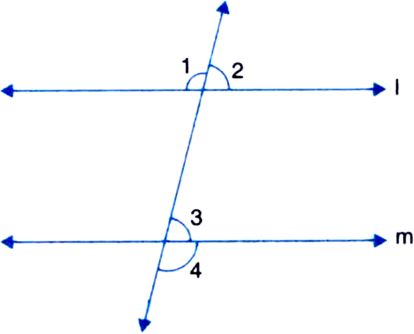
Solution not provided.
Ans. 80°, 100°
In figure, if PQ || RS and ∠PXM = 50° and ∠MYS = 120°, find the value of x.
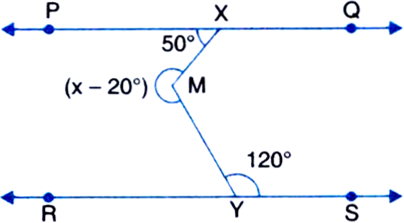
Solution not provided.
Ans. 270°
In figure, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.

Solution not provided.
Ans. 50°, 77°
In figure, PQ || RS, ∠PAB = 80° and ∠ACS = 120°. Find the value of x.
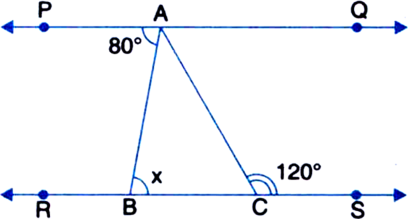
Solution not provided.
Ans. 80°
In figure, sides QP and RQ of ∆PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°. find ∠PRQ.
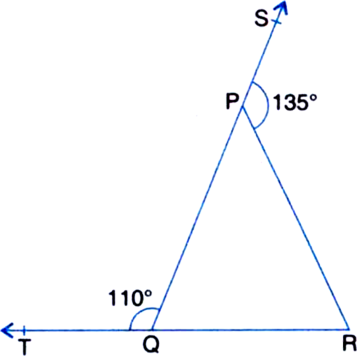
∵ TR is a line
∴ ∠PQT + ∠PQR = 180°
⇒ 110° + ∠PQR = 180°
⇒ ∠PQR = 180° - 110° = 70° ...(1)
∵ QS is a line
∴ ∠SPR + ∠QPR = 180°
⇒ 135° + ∠QPR = 180°
⇒ ∠QPR = 180° - 135° = 45° ...(2)
In ∆PQR,
∠PQR + ∠QPR + ∠PRQ = 180°
| ∵ The sum of all the angles of a triangle is 180°
⇒ 70° + 45° + ∠PRQ = 180°
| Using (1) and (2)
⇒ 115° + ∠PRQ = 180°
⇒ ∠PRQ = 180° - 115° = 65°.
In figure, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ∆XYZ, find ∠OZY and ∠YOZ.
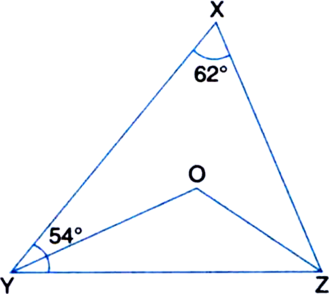
In ∆XYZ,
∠XYZ + ∠YZX + ∠ZXY = 180°
| ∵ The sum of all the angles of a triangle is 180°
⇒ 54° + ∠YZX + 62° = 180°
⇒ 116° + ∠YZX = 180°
⇒ ∠YZX = 180° - 116° = 64° ...(1)
∵ YO is the bisector of ∠XYZ
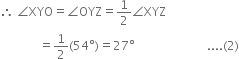
∵ ZO is the bisector of ∠YZX
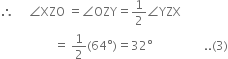
In ∆OYZ,
∠OYZ + ∠OZY + ∠YOZ = 180°
|∵ The sum of all the angles of a triangle is 180°
⇒ 27° + 32° + ∠YOZ = 180°
| Using (2) and (3)
⇒ 59° + ∠YOZ = 180°
⇒ ∠YOZ = 180° - 59° = 121°.
In figure, if AB || DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.
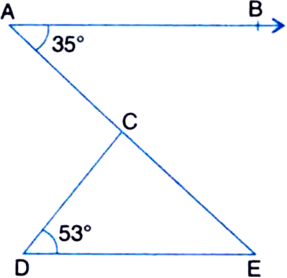
∠DEC = ∠BAC = 35° ...(1)
| Alternate Interior Angles
∠CDE = 53° ...(2) | Given
In ∆CDE,
∠CDE + ∠DEC + ∠DCE = 180°
| ∵ The sum of all the angles of a triangle is 180°.
⇒ 53°+ 35° + ∠DCE = 180°
| Using (1) and (2)
⇒ 88° + ∠DCE = 180°
⇒ ∠DCE = 180° - 88° = 92°.
In figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.

In ∆PRT,
∠PTR + ∠PRT + ∠RPT = 180°
| ∵ The sum of all the angles of a triangle is 180°
⇒ ∠PTR + 40°+ 95° = 180°
⇒ ∠PTR + 135° = 180°
∠ ∠PTR = 45°
⇒ ∠QTS = ∠PTR = 45°
| Vertically Opposite Angles
In ∆TSQ,
∠QTS + ∠TSQ + ∠SQT = 180°
| ⇒ The sum of all the angles of a triangle is 180°
⇒ 45° + 75° + ∠SQT = 180°
⇒ 120° + ∠SQT = 180°
⇒ ∠SQT = 180° - 120° = 60°.
In figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.
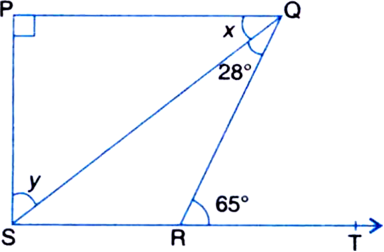
∠QRT = ∠RQS + ∠QSR
| ∵ The exterior angle is equal to the sum of the two interior opposite angles. ⇒ 65°
= 28° + ∠QSR
⇒ ∠QSR = 65° - 28° = 37°
∵ PQ ≠ SP
∴ ∠QPS = 90°
∵ PQ || SR
∴ ∠QPS + ∠PSR = 180°
| ∵ The sum of consecutive interior angles on the same side of the transversal is 180°
⇒ 90° + ∠PSR = 180°
⇒ ∠PSR = 180° - 90° = 90°
⇒ ∠PSQ + ∠QSR = 90°
⇒ y + 37° = 90°
⇒ y = 90° - 37° = 53°
In ∆PQS,
∠PQS + ∠QSP + ∠QPS = 180°
| ∵ The sum of all the angles of a triangle is 180°
⇒ x + y + 90° = 180°
⇒ x + 53° + 90° = 180°
⇒ x + 143° = 180°
⇒ x = 180° - 143° = 37°.
In figure, the side QR of ∆PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that
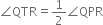
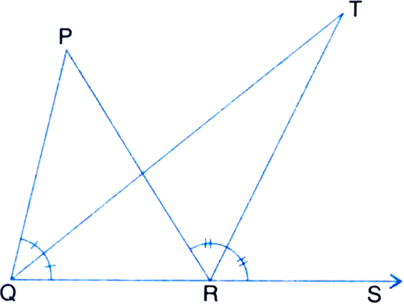
∵ ∠TRS is an exterior angle of ∆TQR ∴ ∠TRS = ∠TQR + ∠QTR ...(1)
| ∵ The exterior angle is equal to sum of its two interior opposite angles
∵ ∠ PRS is an exterior angle of ∆PQR
∴ ∠PRS = ∠PQR + ∠QPR ...(2)
| ∵ The exterior angle is equal to the sum of its two interior opposite angles
⇒ 2 ∠TRS = 2∠TQR + ∠QPR
| ∵ QT is the bisector of ∠PQR and RT is the bisector of ∠PRS
⇒ 2(∠TRS - ∠TQR) = ∠QPR ...(3)
From (1),
∠TRS - ∠TQR = ∠QTR ...(4)
From (3) and (4), we obtain
![]()
Prove that if one angle of a triangle is equal to the sum of the other two angles, the triangle is right angled.
Let in ∆ABC,
∠A = ∠B + ∠C ...(1)
We know that,
∠A + ∠B + ∠C = 180°
| ∵ The sum of the three angles of a triangle is 180°
⇒ ∠A + ∠A = 180° | From (1)
⇒ 2 ∠A = 180°![]()
Hence triangle ABC is right angled triangle.
In figure, the bisectors of ∠ABC and ∠BCA intersect each other at the point O. Prove that 
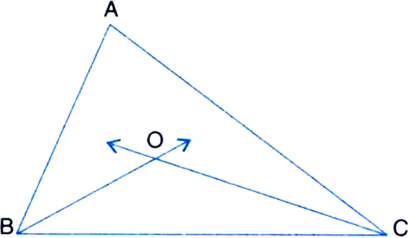
∵ CO is the bisector of ∠ACB
In ∆OBC, ∠BOC + ∠OBC + ∠OCB = 180°
| ∵ The sum of the three angles of a ∆ is 180°![]()
| From (1) and (2)![]()
In ∠ABC, ∠A + ∠B + ∠C = 180°
| ∵ The sum of the three angles of a triangle is 180°
From (3) and (4), we have![]()
The side EF, FD and DE of a triangle DEF are produced in order forming three exterior angles DFP, EDQ and FER respectively. Prove that
∠DFP + ∠EDQ + ∠FER = 360°.
OR
Prove that the sum of the exterior angles of a triangl is 360°.
∠DFP = ∠D + ∠E ...(1)
| Exterior Angle Theorem
∠EDQ = ∠E + ∠F ...(2)
| Exterior Angle Theorem
∠FER = ∠F + ∠D ...(3)
| Exterior Angle Theorem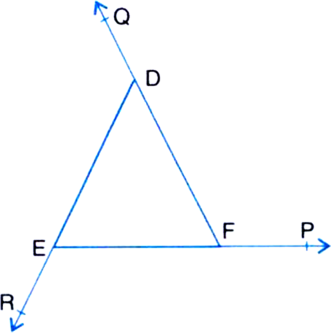
Adding (1), (2) and (3), we get
∠DFP + ∠EDQ + ∠FER = 2(∠D + ∠E + ∠F)
But ∠D + ∠E + ∠F = 180°
| ∵ The sum of the three angles of a triangle is 180°
∴ ∠DFP + ∠EDQ + ∠FER = 2(180°) = 360°.
In the figure, AD and CE are the angle bisectors of ∠A and ∠C respectively. If ∠ABC = 90° then find ∠AOC.
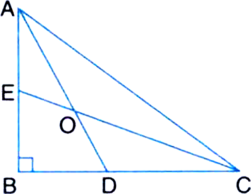
Given: AD and CE are the angle bisectors of ∠A and ∠C respectively. ∠ABC = 90°
To Determine: ∠AOC
Determination: In ∆ABC,
∠A + ∠B + ∠C = 180°
| Angles sum property of a triangle
⇒ ∠A + 90° + ∠C = 180°
⇒ ∠A + ∠C = 90° ...(1)
In ∆AOC,
∠OAC + ∠OCA + ∠AOC = 180°
| Angle sum property of a triangle
In figure, find the value of x.
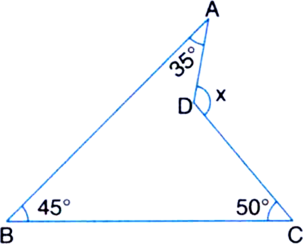
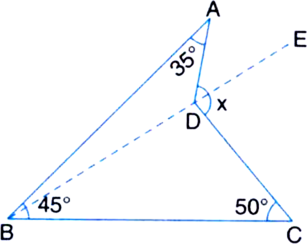
Construction: Join BD and extend upto E.
x = ∠ADC
= ∠ADE + ∠CDE
= (∠DAB + ∠ABD) + (∠DBC + ∠DCB)
| Exterior angle theorem
= 35° + (∠ABD + ∠DBC) + 50°
= 35° + ∠ABC + 50°
= 35° + 45° + 50°
= 130°
In figure, if QT ⊥ PR, ∠TQR = 40° and ∠SPR = 30°, find the value of x and y.
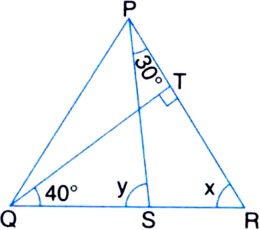
In ∆QTR,
∠QTR + ∠r + 40° = 180°
| ∠ Angle sum property of a triangle
⇒ 90° + ∠x + 40° = 180°
⇒ ∠r + 130° = 180°
⇒ ∠x = 180° - 130° = 50°
∠x = 50°
In ∠PSR,
y° = x° + 30°
| Exterior angle theorem
= 50° + 30°
= 80°
⇒ y = 80°
In figure, if line segment AB intersects CD at O such that ∠OAD = 80°, ∠ODA = 50° and ∠OCB = 40°, then find ∠OBC.

In ∆OAD,
∠OAD + ∠ODA + ∠AOD = 180°
| Angle sum property of a triangle
⇒ 80° + 50° + ∠AOD = 180°
⇒ 130° + ∠AOD = 180°
⇒ ∠AOD = 180° - 130° = 50°
⇒ ∠BOC = 50°
| ∵ ∠AOD = ∠BOC (Vertically opposite angles)
In ∆OBC,
∠BOC + ∠OCB + ∠OBC = 180°
| Angle sum property of a triangle ⇒ 50° + 40° + ∠OBC = 180°
⇒ 90° + ∠OBC = 180°
∠ ∠OBC = 180° - 90° = 90°
In figure, AP and DP are bisectors of two adjacent angles A and D of a quadrilateral ABCD. Prove that 2 ∠APD = ∠B + ∠C.
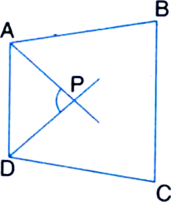
Given: AP and DP are bisectors of two adjacent angles A and D of a quadrilateral ABCD.
To Prove: 2 ∠APD = ∠B + ∠C
Proof: We know that the sum of all the angles of a quadrilateral is 360°. So,
∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠A + ∠D = 360° - (∠B + ∠C) ...(1)
Now, in ∆PAD,
∠APD + ∠PAD + ∠PDA = 180°
| Angle sum property of a triangle![]()
∵ AP and DP are the bisectors of two adjacent angles A and D of quadrilateral ABCD
⇒ 2 ∠APD + ∠A + ∠D = 360°
⇒ 2 ∠APD = 360° - (∠A + ∠D)
⇒ 2∠APD = ∠B + ∠C
In figure, AB II DE, ∠ABC = 75°, ∠CDE = 145°, find ∠BCD.
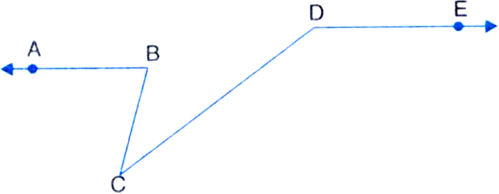
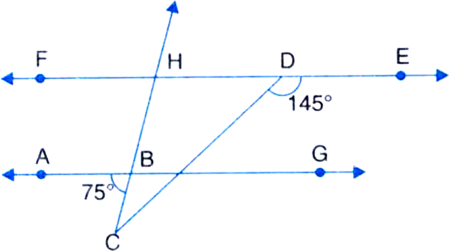
Construction: Extend ED, AB and CB.
∠BHF = ∠CBA
| Corresponding angles
∵ AB || FE and BH intersects them
= 75° ...(1)
∠BHF + ∠BHD = 180° | Linear pair axiom
⇒ 75° + ∠BHD = 180°
⇒ ∠BHD = 105° ...(2)
∠CDH + ∠CDE = 180° | Linear pair axiom
⇒ ∠CDH + 145° = 180°
⇒ ∠CDH = 35° ...(3)
In ∆CHD,
∠CDH + ∠CHD + ∠BCD = 180°
| Angle sum property of a triangle
⇒ 35° + 105° + ∠BCD = 180°
⇒ ∠BCD = 40°
In figure, the side BC of ∆ABC is produced to D. The bisector of ∠A meets BC in L. Prove that ∠ABC + ∠ACD = 2 ∠ALC
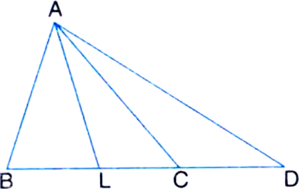
Given: The side BC of ∆ABC is produced to D. The bisector of ∠A meets BC in L.
To Prove: ∠ABC + ∠ACD = 2 ∠ALC.
Proof: ∠ABC + ∠ACD
= ∠ABC + (∠ABC + ∠BAC)
| Exterior angle theorem
= 2 ∠ABC + ∠BAC
= 2 ∠ABC + 2 ∠BAL
| ∵ AL is the bisector of ∠A
= 2 (∠ABC + ∠BAL)
= 2 ∠ALC | Exterior angle theorem
Prove that the sum of the angles of a hexagon is 720°.
Given: A hexagon ABCDEF
To Prove:
∠ A + ∠B + ∠C + ∠D + ∠E + ∠F = 720°
Construction: Join AD, BE and FC so as to intersect at O.
Proof: In ∆OAB,
∠1 + ∠7 + ∠9 = 180° ...(1)
| Angle sum property of a triangle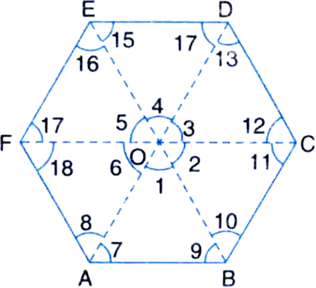
In ∆AOBC,
∠2 + ∠10 + ∠11 = 180° ...(2)
| Angle sum property of a triangle
In ∆OCD,
∠3 + ∠12 + ∠13 = 180° ...(3)
| Angle sum property of a triangle
In ∆CDE,
∠4 + ∠14 + ∠15 = 180° ...(4)
| Angle sum property of a triangle
In ∆OEF,
∠5 + ∠16 + ∠17 = 180° ...(5)
| Angle sum property of a triangle
In ∆OFA,
∠6 + ∠18 + ∠8 = 180° ...(6)
| Angle sum property of a triangle
Adding (1), (2), (3), (4), (5) and (6), we get
(∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6)
+ (∠7 + ∠8) + (∠9 + ∠10)
+ (∠11 + ∠12) + (∠13 + ∠14)
+ (∠15 + ∠16) + (∠17 + ∠18)
=1080°
⇒ 360° + ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 1080°
| ∵ Sum of all the angles round a point is equal to 360°
⇒ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 1080° - 360° = 720°
In figure, PS is the bisector of ∠QPR and PT ⊥ QR. Show that 
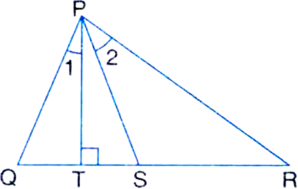
Given: PS is the bisector of ∠PQR and PT⊥QR.
To Prove: ![]()
Proof: ∵ PS is the bisector of ∠QPR
∴ ∠QPS = ∠RPS
⇒ ∠1 + ∠TPS = ∠2 ...(1)
In ∆PQT,
∠PTQ = 90° | Given
∴ ∠1 + ∠Q = 90°
| Angle sum property of a triangle
⇒ ∠Q = 90° - ∠1 ...(2)
In ∆PRT,
∠PTR = 90° | Given
∴ ∠R + ∠TPR = 90°
| Angle sum property of a triangle
⇒ ∠R + (∠TPS + ∠2) = 90° ...(3)
From (2) and (3),
∠Q = ∠R + (∠TPS + ∠2) - ∠1
⇒ ∠Q - ∠R = ∠TPS + (∠2 - ∠1)
⇒ ∠Q - ∠R = ∠TPS + ∠TPS | From (1) ⇒ ∠Q - ∠R = 2 ∠TPS![]()
ABC is a triangle right angled at A. AL is drawn perpendicular to BC. Show that ∠BAL = ∠ACB.
Given: ABC is a triangle right angled at A. AL is drawn perpendicular to BC.
To Prove: ∠BAL = ∠ACB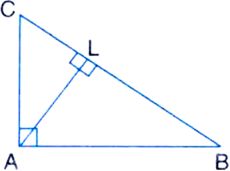
Proof: In triangle ALB,
∠ALB + ∠BAL + ∠ABL = 180°
| Angle sum property of a triangle
⇒ 90° + ∠BAL + ∠ABC = 180°
⇒ ∠BAL + ∠ABC = 90° ...(1)
In triangle ABC,
∠BAC + ∠ACB + ∠ABC = 180°
| Angle sum property of a triangle
⇒ 90° + ∠ACB + ∠ABC = 180°
⇒ ∠ACB + ∠ABC = 90° ...(2)
From (1) and (2),
∠BAL + ∠ABC = ∠ACB + ∠ABC
⇒ ∠BAL = ∠ACB
Sponsor Area
Prove that the sum of all the angles of a quadrilateral is 360°.
Given: ABCD is a quadrilateral
To Prove: ∠A + ∠B + ∠C + ∠D = 360°
Construction: Join AC.
Proof: In ∆ABC,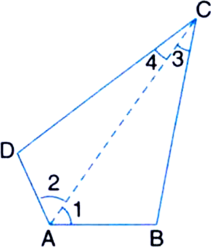
∠1 + ∠B + ∠3 = 180° ...(1)
| Angle sum property of a triangle
In ∆ADC,
∠2 + ∠D + ∠4 = 180° ...(2)
| Angle sum property of a triangle
Adding (1) and (2), we get
(∠1 + ∠2) + ∠B + (∠3 + ∠4) + ∠D = 360°
∠ ∠A + ∠B + ∠C + ∠D = 360°
In figure, the side BC of a ∆ABC is produced to D. The bisector of ∠BAC intersects the side BC at E. Prove that ∠ABC + ∠ACD = 2 ∠AEC.
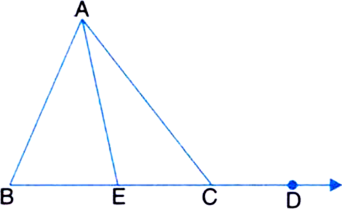
Given: The side BC of a ∆ABC is produced to D. The bisector of ∠BAC intersects the side BC at E.
To Prove: ∠ABC + ∠ACD = 2 ∠AEC.
Proof: In ∆ABE,
∠AEC = ∠ABC + ∠BAE
| Exterior angle theorem
= ∠ABC + ∠CAE ...(1)
| ∠BAE = ∠CAE (∵ AE bisects ∠BAC)
In ∆AEC,
∠ACD = ∠AEC + ∠CAE
| Exterior angle theorem
⇒ ∠CAE = ∠ACD - ∠AEC ...(2)
From (1) and (2),
∠AEC = ∠ABC + (∠ACD - ∠AEC)
⇒ 2 ∠AEC = ∠ABC + ∠ACD
The sides BA and DC of a quadrilateral ABCD are produced as shown in figure. Show that ∠x + ∠y = ∠a + ∠b
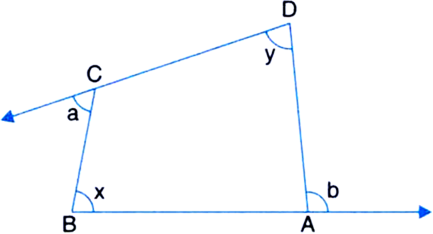
Given: The sides BA and DC of a quadrilateral ABCD are produced.
To Prove: ∠x + ∠y = ∠a + ∠b
Construction: Join BD
Proof: In ∆BCD,
∠a = ∠2 + ∠4 ...(1)
| Exterior angle theorem
In ∆ADB,
∠b = ∠1 + ∠3 ...(2)
| Exterior angle theorem
Adding (1) and (2), we get
∠a + ∠b = (∠1 + ∠2) + (∠3 + ∠4)
⇒ ∠a + ∠b - ∠x + ∠y
The degree measures of three angles of a triangle are x, y and z. If 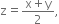 then find the value of z.
then find the value of z.
∵ x, y and z are the degree measures of three angles of a triangle
∴ x + y + z = 180°
| Angle sum property of a triangle![]()
| Dividing throughout by 2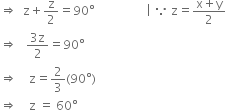
The angles of a triangle are 2x + 35, 3x - 5 and 5x - 50 degree. Find x.
Solution not provided.
Ans. 20°
The sum of two angles of a triangle is 80° and the difference is 20°. Find all the angles of the triangle.
Solution not provided.
Ans. 50°, 30°, 100°,
In the figure, ∠X = 72°, ∠X ZY = 46°. If YO and ∠O are bisectors of ∠XYZ and ∠XZY respectively of ∆XYZ, find ∠OYZ and ∠YOZ.
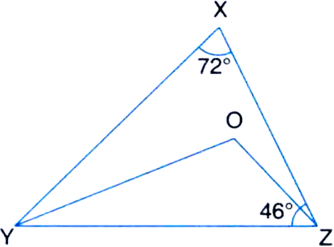
Solution not provided.
Ans. 41°, 116°
In figure, AB || DC, ∠BDC = 30° and ∠BAD = 80°, find ∠x, ∠y and ∠z.
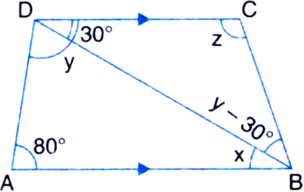
Solution not provided.
Ans. 30°, 70°, 110°
In figure, TQ, TR are the bisectors of ∠Q and ∠R respectively. ∠QPR = 80°, ∠PRT = 30°, determine ∠TQR and ∠QTR.
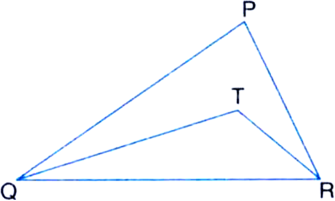
Solution not provided.
Ans. 20°, 130°
An exterior angle of a triangle is 120° and one of the interior opposite angles is 40°. Find the other two angles of a triangle.
Solution not provided.
Ans. 80°, 60°
The exterior angles obtained on producing the base of a triangle both ways are 100° and 120°. Find all the angles.
Solution not provided.
Ans. 80°, 60°, 40°
In figure, PQ || SR, ∠SQR = 25°, ∠QRT = 65°, find x and y:
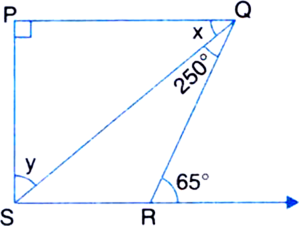
Solution not provided.
Ans. 55°, 25°
If the angles of a triangle are in the ratio 1 : 2 : 3. Then find the measure of angles.
Solution not provided.
Ans. 30°, 60°. 90°
In ∆ABC. ∠B = 35°, ∠C = 65° and bisector of ∠A meets BC at point D. Find ∠ADB and ∠ADC.
Solution not provided.
Ans. 105°, 75°
In figure, BP⊥AC, ∠PBC = 25° and ∠DAC = 30°. Find the value of x.
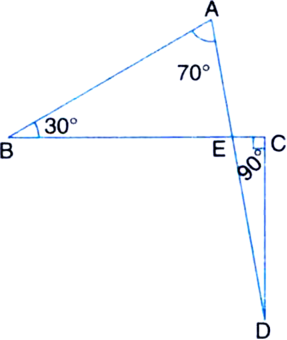
Solution not provided.
Ans. 95°
In figure, if AB || CD, ∠FAE = 90° and ∠AFE = 40° then find ∠ECD.
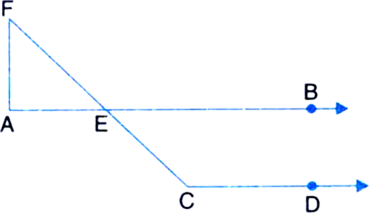
Solution not provided.
Ans. 130°
In figure, BO and CO are the bisectors of ∠DBC and ECB respectively. If ∠BAC = 50° and ∠ABC = 60°, then find the measure of ∠BOC.
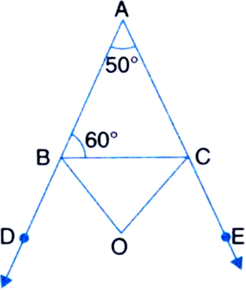
Solution not provided.
Ans. 65°
In figure, ∠B = 55°, ∠C = 45° and the bisector of ∠A meets BC at D. Find ∠ADB and ∠ADC.
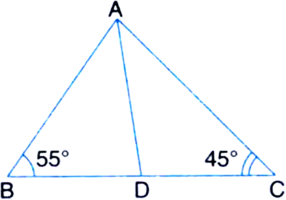
Solution not provided.
Ans. 85°, 95°
An acute angle
-
measures between 0° and 90°
-
is exactly equal to 90°
-
is greater than 90° but less than 180°
-
is equal to 180°
A.
measures between 0° and 90°
A right angle
-
measures between 0° and 90°
-
is exactly equal to 90°
-
is greater than 90° but less than 180°
-
is equal to 180°
B.
is exactly equal to 90°
An obtuse angle
-
measures between 0° and 90°
-
is greater than 90° but less than 180°
-
is exactly equal to 90°
-
is exactly equal to 180°
B.
is greater than 90° but less than 180°
A straight angle
-
is greater than 90° but less than 180°
-
is exactly equal to 90°
-
measures between 0° and 90°
-
is exactly equal to 180°
D.
is exactly equal to 180°
An angle which is exactly equal to 180° is called
-
a right angle
-
a straight angle
-
an acute angle
-
an obtuse angle
B.
a straight angle
A reflex angle
-
is greater than 180° but less than 360°
-
is exactly equal to 180°
-
is exactly equal to 90°
-
is greater than 90° but less than 180°
A.
is greater than 180° but less than 360°
Two angles whose sum is 90° are called
-
supplementary angles
-
complementary angles
-
corresponding angles
-
alternate angles
B.
complementary angles
The angles whose sum is 180° are called
-
supplementary angles
-
complementary angles
-
alternate angles
-
corresponding angles
A.
supplementary anglesSponsor Area
The sum of the three angles of a triangle is
-
one right angle
-
two right angles
-
three right angles
-
four right angles
B.
two right angles
If two parallel lines are cut by a transversal, then which of the following is not true?
-
Corresponding angles are equal
-
Alternate interior angles are equal
-
Interior angles of the same side of the transversal are supplementary
-
Interior angles on the same side of the transversal are complementary.
D.
Interior angles on the same side of the transversal are complementary.
A triangle can have:
-
Two right angles
-
Two obtuse angles
-
All angles more than 60°
-
Two acute angles
D.
Two acute angles
The exterior angle of a triangle is equal to the sum of two:
-
Exterior angles
-
Interior angles
-
Interior opposite angles
-
Alternate angles
C.
Interior opposite angles
In figure, find the values of x and y and then show that AB || CD.
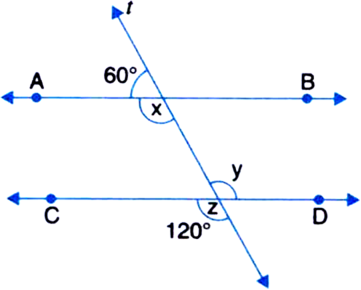
Solution not provided.
Ans. 140°, 140°, 140°
Let OA, OB, OC and OD be the rays in the anticlockwise direction starting from OA, such that ∠AOB = ∠COD = 100°, ∠AOD = ∠BOC = 80°. Is it true that AOC and BOD are straight lines? Justify your answer by drawing the figure.
Solution not provided.
Ans. AOC is a straight line but not BOD
In figure, if AB || DC, ∠BDC = 30° and ∠BAD = 80°, find ∠x, ∠y and ∠z.
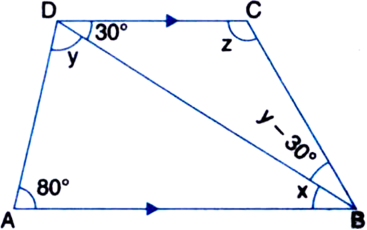
Solution not provided.
Ans. 30°, 70°, 110°
The side BC of ∆ABC is produced on both sides. Prove that the sum of the two exterior angles so formed is greater than ∠A by 180°.
Solution not provided.
Ans. 90° 13. 110°
An angle is equal to five times its supplement. Find the measure of the angle.
Solution not provided.
Ans. 15°
In the figure, PQ ⊥ QS. Find ‘x’ and ‘y’ where ∠PRS = 120° and ∠PSR = 30°.
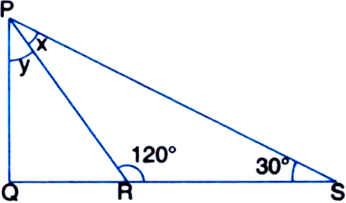
Solution not provided.
Ans. 30°, 30°
Mock Test Series
Sponsor Area
Sponsor Area