Sponsor Area
Lines And Angles
Question
Prove “if two lines intersect each other, then the vertically opposite angles are equal.”
Solution
Let AB and CD be two lines intersecting at O.
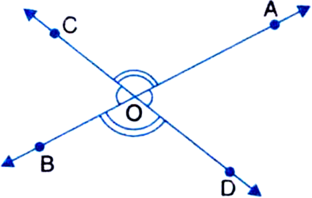
This leads to two pairs of vertically opposite angles, namely,
(i) ∠AOC and ∠BOD
(ii) ∠AOD and ∠BOC
We are to prove that
(i) ∠AOC = ∠BOD
and (ii) ∠AOD = ∠BOC
∵ Ray OA stands on line CD Therefore,
∠AOC + ∠AOD = 180° ...(1)
| Linear Pair Axiom
∵ Ray OD stands on line AB Therefore,
∠AOD + ∠BOD = 180° ...(2)
| Linear Pair Axiom
From (1) and (2),
∠AOC + ∠AOD = ∠AOD + ∠BOD
⇒ ∠AOC = ∠BOD
Similarly, we can prove that
∠AOD = ∠BOC
Some More Questions From Lines and Angles Chapter
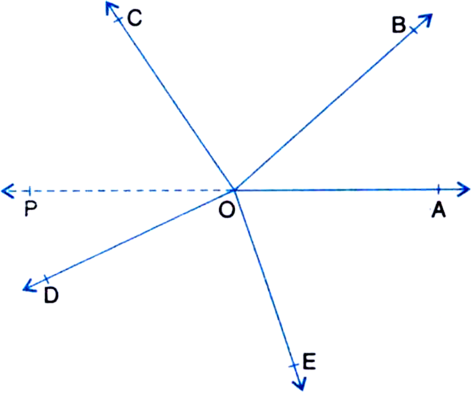
Rays OA, OB. OC, OD and OE have the common initial point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.
Prove “if two lines intersect each other, then the vertically opposite angles are equal.”
In figure, OP bisects ∠AOC, OQ bisects ∠BOC and OP ⊥ OQ. Show that the points A, O and B are collinear.
In figure, if y = 20°, prove that the line AOB is a straight line.
In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex angle EOC.
In figure, lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ = 5 : 7, find all the angles.
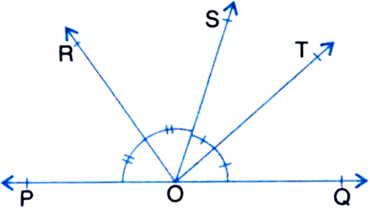
In figure, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ, respectively. If ∠POS = x, find ∠ROT.
If the complement of an angle is one-third of its supplement, find the angle.
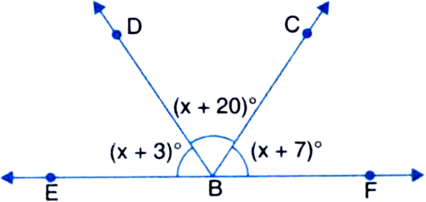
In figure, find the value of x.
In figure, if ∠POR and ∠QOR form a linear pair and a - b = 80° then find the value of a and b.
Sponsor Area
Mock Test Series
Mock Test Series