Sponsor Area
Lines And Angles
Question
In figure, if y = 20°, prove that the line AOB is a straight line.


Solution
∵ Sum of all the angle round a point is equal to 360°.
∴ y + (3x - 15) + (y + 5) + 2y + (4y + 10) + x = 360°
⇒ 4x + 8y = 360°
⇒ x + 2y = 90°
⇒ x + 2(20°) = 90°
⇒ x + 40° = 90°
⇒ x = 50°
Now, y + 3x - 15 + y + 5 = 3x + 2y - 10
= 3(50°) + 2(20°) - 10
= 150° + 40° - 10°
= 180°
∴ AOB is a straight line.
Some More Questions From Lines and Angles Chapter
In figure, OP bisects ∠AOC, OQ bisects ∠BOC and OP ⊥ OQ. Show that the points A, O and B are collinear.

In figure, if y = 20°, prove that the line AOB is a straight line.


In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex angle EOC.

In figure, lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ = 5 : 7, find all the angles.

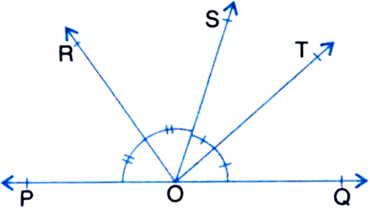
In figure, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ, respectively. If ∠POS = x, find ∠ROT.
If the complement of an angle is one-third of its supplement, find the angle.
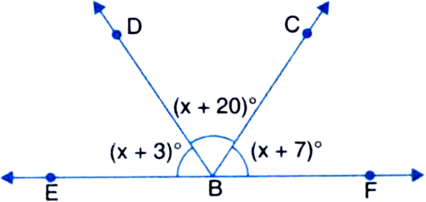
In figure, find the value of x.
In figure, if ∠POR and ∠QOR form a linear pair and a - b = 80° then find the value of a and b.

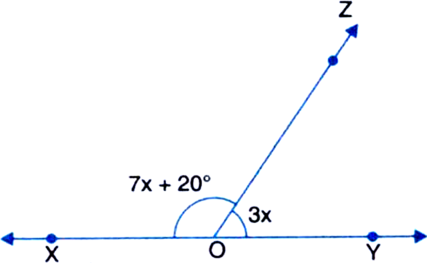
What value of x would make XOY a line if ∠XOZ = 7x + 20° and ∠YOZ = 3x in figure.
Sponsor Area
Mock Test Series
Mock Test Series





