Sponsor Area
Lines And Angles
Question
In figure, OP bisects ∠AOC, OQ bisects ∠BOC and OP ⊥ OQ. Show that the points A, O and B are collinear.

Solution
Given: OP bisects ∠AOC, OQ bisects ∠BOC and OP ⊥ OQ.
To Prove: The points A, O and B are collinear.
Proof: ∵ OP bisects ∠AOC
∴ ∠AOP = ∠COP ...(1)
∵ OQ bisects ∠BOC
∠BOQ = ∠COQ ...(2)
Now, ∠AOB
= ∠AOP + ∠COP + ∠COQ + ∠BOQ
= ∠COP + ∠COP + ∠COQ + ∠COQ
| From (1) and (2)
= 2(∠COP + ∠COQ)
= 2 ∠POQ
= 2(90°) | ∵ OP ⊥ OQ
= 180°
∴ The points A, O and B are collinear.
| By converse of Linear Pair Axiom
Some More Questions From Lines and Angles Chapter
Prove “if two lines intersect each other, then the vertically opposite angles are equal.”
In figure, OP bisects ∠AOC, OQ bisects ∠BOC and OP ⊥ OQ. Show that the points A, O and B are collinear.

In figure, if y = 20°, prove that the line AOB is a straight line.


In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex angle EOC.

In figure, lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ = 5 : 7, find all the angles.

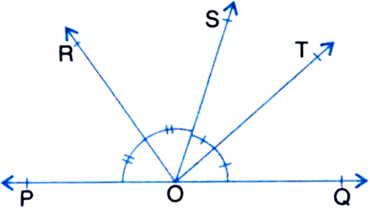
In figure, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ, respectively. If ∠POS = x, find ∠ROT.
If the complement of an angle is one-third of its supplement, find the angle.
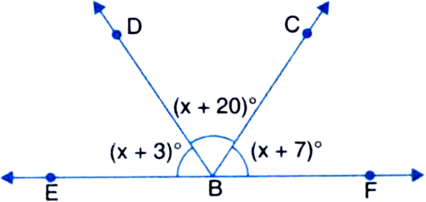
In figure, find the value of x.
In figure, if ∠POR and ∠QOR form a linear pair and a - b = 80° then find the value of a and b.

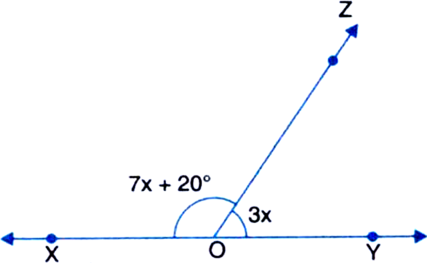
What value of x would make XOY a line if ∠XOZ = 7x + 20° and ∠YOZ = 3x in figure.
Sponsor Area
Mock Test Series
Mock Test Series





