+91-8076753736[email protected]
logo
logo
-->

Lines And Angles

Question
CBSEENMA9002410
Wired Faculty App

In figure, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ∆XYZ, find ∠OZY and ∠YOZ.

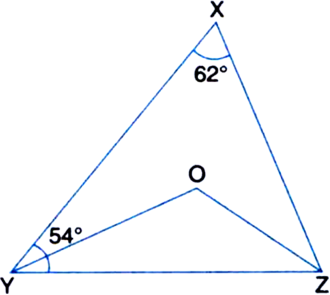
Solution

In ∆XYZ,
∠XYZ + ∠YZX + ∠ZXY = 180°
| ∵ The sum of all the angles of a triangle is 180°
⇒ 54° + ∠YZX + 62° = 180°
⇒    116° + ∠YZX = 180°
⇒ ∠YZX = 180° - 116° = 64°    ...(1)
∵ YO is the bisector of ∠XYZ

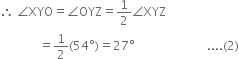
therefore space angle XYO equals angle OYZ equals 1 half angle XYZ space space space space space space space space space space space space space equals 1 half left parenthesis 54 degree right parenthesis equals 27 degree space space space space space space space space space space space space space space space space space space space space space space space space.... left parenthesis 2 right parenthesis
∵ ZO is the bisector of ∠YZX
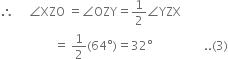
therefore space space space space space angle XZO space equals angle OZY equals 1 half angle YZX space space space space space space space space space space space space space space space space space space equals space 1 half left parenthesis 64 degree right parenthesis equals 32 degree space space space space space space space space space space space space space space space space space.. left parenthesis 3 right parenthesis
                                                   | Using (1)

In ∆OYZ,
∠OYZ + ∠OZY + ∠YOZ = 180°
|∵ The sum of all the angles of a triangle is 180°
⇒ 27° + 32° + ∠YOZ = 180°
| Using (2) and (3)
⇒ 59° + ∠YOZ = 180°
⇒    ∠YOZ = 180° - 59° = 121°.


Some More Questions From Lines and Angles Chapter

Ray OE bisects ∠AOB and OF is the ray opposite to OE. Show that ∠FOB = ∠FOA.

Rays OA, OB. OC, OD and OE have the common initial point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.

Prove “if two lines intersect each other, then the vertically opposite angles are equal.”

In figure, OP bisects ∠AOC, OQ bisects ∠BOC and OP ⊥ OQ. Show that the points A, O and B are collinear.

In figure, if y = 20°, prove that the line AOB is a straight line.

In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex angle EOC.

In figure, lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ = 5 : 7, find all the angles. 

In figure, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ, respectively. If ∠POS = x, find ∠ROT.

If the complement of an angle is one-third of its supplement, find the angle. 

In figure, find the value of x.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation