Sponsor Area
Lines And Angles
Question
Ray OE bisects ∠AOB and OF is the ray opposite to OE. Show that ∠FOB = ∠FOA.
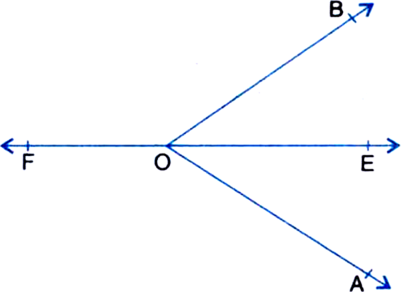
Solution
∠FOB + ∠BOE = 180° ...(1)
| Linear Pair Axiom
∠FOA + ∠AOE = 180° ...(2)
| Linear Pair Axiom
From (1) and (2),
∠FOB + ∠BOE = ∠FOA + ∠AOE ...(3)
But ∠BOE = ∠AOE
| ∵ Ray OE bisects ∠AOB
∴ From (3),
⇒ ∠FOB = ∠FOA.
Some More Questions From Lines and Angles Chapter
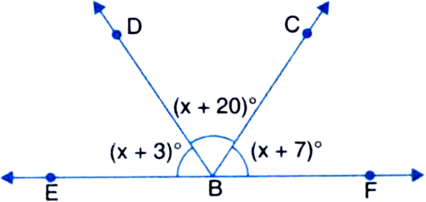
In figure, find the value of x.
In figure, if ∠POR and ∠QOR form a linear pair and a - b = 80° then find the value of a and b.

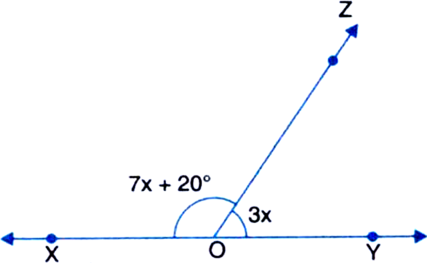
What value of x would make XOY a line if ∠XOZ = 7x + 20° and ∠YOZ = 3x in figure.
Two supplementary angles are in the ratio 4 : 5. Find the angles.
In figure, lines AB and CD intersect at O. If ∠AOD : ∠DOC = 4 : 5 then find ∠COB.

An angle is equal to five times of its complement. Find the measure of the angle.
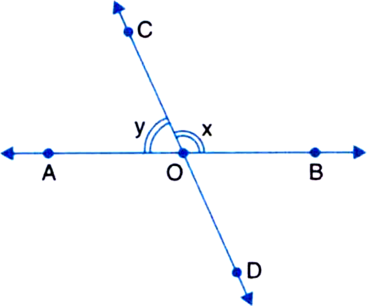
In figure, lines I and m intersect each other at O. If x = 40°, then, find the values of y, z and w.

If OA, OB. OC and OD are the rays such that ∠AOB = ∠COD = 150°, ∠BOC = 30° and ∠AOD = 30°. Is it true that AOC and BOD are straight lines? Justify your answer.

In figure, angles x and y are supplementary angles. If ∠x = 110°, find the value of y.
Sponsor Area
Mock Test Series
Mock Test Series





