Question
In figure, the bisectors of ∠ABC and ∠BCA intersect each other at the point O. Prove that 
Solution
∵ BO is the bisector of ∠ABC.

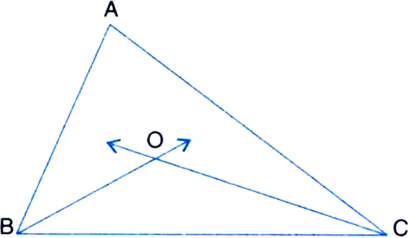
∵ CO is the bisector of ∠ACB
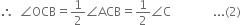

∵ CO is the bisector of ∠ACB
In ∆OBC, ∠BOC + ∠OBC + ∠OCB = 180°
| ∵ The sum of the three angles of a ∆ is 180°![]()
| From (1) and (2)![]()
In ∠ABC, ∠A + ∠B + ∠C = 180°
| ∵ The sum of the three angles of a triangle is 180°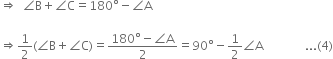
From (3) and (4), we have![]()