Question
In figure, PQ || RS and T is any point as shown in the figure then show that
∠PQT + ∠QTS + ∠RST = 360°.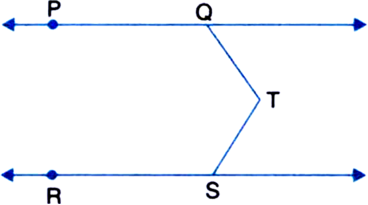
Solution
Given: PQ || RS and T is any point.
To Prove: ∠PQT + ∠QTS + ∠RST = 360°
Construction: Through T, draw TU || PQ || RS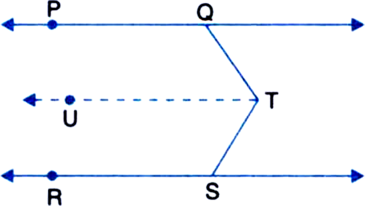
Proof: ∵ PQ || UT | By construction and a transversal QT intersects then
∴ ∠PQT + ∠QTU = 180° ...(1)
| Sum of consecutive interior angles on the same sides of a transversal is 180°
∵ UT || RS | By construction and a transversal TS intersects them
∴ ∠UTS + ∠RST = 180° ...(2)
| Sum of consecutive interior angles on the same side of a transversal is 180°
Adding (1) and (2), we get
∠PQT + (∠QTU + ∠UTS) + ∠RST = 360°
⇒ ∠PQT + ∠QTS + ∠RST = 360°
