Question
In figure, sides QP and RQ of ∆PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°. find ∠PRQ.
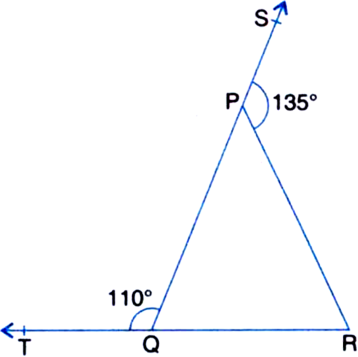
Solution
∵ TR is a line
∴ ∠PQT + ∠PQR = 180°
⇒ 110° + ∠PQR = 180°
⇒ ∠PQR = 180° - 110° = 70° ...(1)
∵ QS is a line
∴ ∠SPR + ∠QPR = 180°
⇒ 135° + ∠QPR = 180°
⇒ ∠QPR = 180° - 135° = 45° ...(2)
In ∆PQR,
∠PQR + ∠QPR + ∠PRQ = 180°
| ∵ The sum of all the angles of a triangle is 180°
⇒ 70° + 45° + ∠PRQ = 180°
| Using (1) and (2)
⇒ 115° + ∠PRQ = 180°
⇒ ∠PRQ = 180° - 115° = 65°.