Question
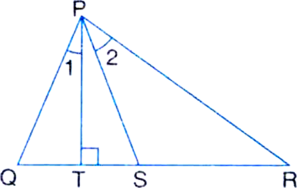
In figure, PS is the bisector of ∠QPR and PT ⊥ QR. Show that 
Solution
Given: PS is the bisector of ∠PQR and PT⊥QR.
To Prove: ![]()
Proof: ∵ PS is the bisector of ∠QPR
∴ ∠QPS = ∠RPS
⇒ ∠1 + ∠TPS = ∠2 ...(1)
In ∆PQT,
∠PTQ = 90° | Given
∴ ∠1 + ∠Q = 90°
| Angle sum property of a triangle
⇒ ∠Q = 90° - ∠1 ...(2)
In ∆PRT,
∠PTR = 90° | Given
∴ ∠R + ∠TPR = 90°
| Angle sum property of a triangle
⇒ ∠R + (∠TPS + ∠2) = 90° ...(3)
From (2) and (3),
∠Q = ∠R + (∠TPS + ∠2) - ∠1
⇒ ∠Q - ∠R = ∠TPS + (∠2 - ∠1)
⇒ ∠Q - ∠R = ∠TPS + ∠TPS | From (1) ⇒ ∠Q - ∠R = 2 ∠TPS![]()