Mathematics Chapter 10 Circles
Sponsor Area
NCERT Solution For Class 9 About 2.html
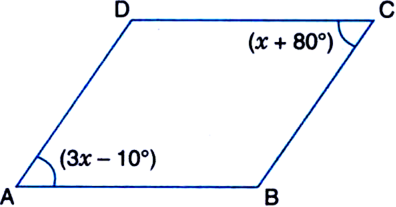
The angles of a quadrilateral are in the ratio 3:5:9: 13. Find all the angles of the quadrilateral.
Let ABCD be a quadrilateral in which
∠A : ∠B : ∠C : ∠D = 3 : 5 : 9 : 13
Sum of the ratios = 3 + 5 + 9+ 13 = 30
Also, ∠A + ∠B + ∠C + ∠D = 360°
Sum of all the angles of a quadrilateral is 360°
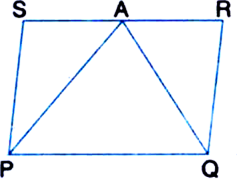
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Given: In parallelogram ABCD, AC = BD.
To Prove: ||gm ABCD is a rectangle.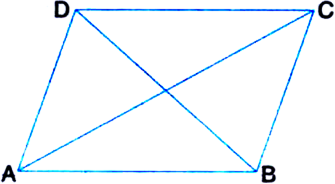
Proof: In ∆ACB and ∆BDA,
AC = BD | Given
AB = BA | Common
BC = AD
| Opposite sides of || gm ABCD
∴ ∆ACB ≅ ∆BDA
| SSS Congruence Rule
∴ ∠ABC = ∠BAD ...(1) C.P.C.T.
Again, ∵ AD || BC
| Opp. sides of || gm ABCD and transversal AB intersects them.
∴ ∠BAD + ∠ABC = 180° ...(2)
| Sum of consecutive interior angles on the same side of a transversal is 180°
From (1) and (2),
∠BAD = ∠ABC = 90°
∴ ∠A = 90°
∴ || gm ABCD is a rectangle.
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Given: ABCD is a quadrilateral whose diagonals AC and BD intersect each other at right angles at O.
To Prove: Quadrilateral ABCD is a rhombus.
Proof: In ∆AOB and ∆AOD,
AO = AO | Common
OB = OD | Given
∠AOB = ∠AOD | Each = 90°
∴ ∆AOB ≅ ∆AOD
| SSS Congruence Rule
∴ AB = AD ...(1) | C.P.C.T.
Similarly, we can prove that
AB = BC ...(2)
BC = CD ...(3)
CD = AD ...(4)
In view of (1), (2), (3) and (4), we obtain
AB = BC = CD = DA
∴ Quadrilateral ABCD is a rhombus.
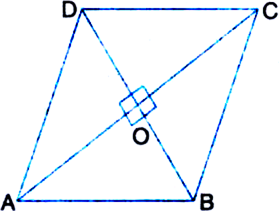
Show that the diagonals of a square are equal and bisect each other at right angles.
Given: ABCD is a square.
To Prove: (i) AC = BD
(ii) AC and BD bisect each other at right angles.
Proof: (i) In ∆ABC and ∆BAD,
AB = BA | Common
BC = AD Opp. sides of square ABCD
∠ABC = ∠BAD | Each = 90°
(∵ ABCD is a square)
∴ ∆ABC ≅ ∆BAD
| SAS Congruence Rule
∴ AC = BD | C.P.C.T
(ii) In ∆OAD and ∆OCB,
AD = CB
| Opp. sides of square ABCD
∠OAD = ∠OCB
| ∵ AD || BC and transversal AC intersects them
∠ODA = ∠OBC
| ∵ AD || BC and transversal BD intersects them
∴ ∆OAD ≅ ∆OCB
| ASA Congruence Rule
∴ OA = OC ...(1)
Similarly, we can prove that
OB = OD ...(2)
In view of (1) and (2),
AC and BD bisect each other.
Again, in ∆OBA and ∆ODA,
OB = OD | From (2) above
BA = DA
| Opp. sides of square ABCD
OA = OA | Common
∴ ∆OBA ≅ ∆ODA
| SSS Congruence Rule
∴ ∠AOB = ∠AOD | C.P.C.T.
But ∠AOB + ∠AOD = 180°
| Linear Pair Axiom
∴ ∠AOB = ∠AOD = 90°
∴ AC and BD bisect each other at right angles.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Given: The diagonals AC and BD of a quadrilateral ABCD are equal and bisect each other at right angles.
To Prove: Quadrilateral ABCD is a square.
Proof: In ∆OAD and ∆OCB,
OA = OC | Given
OD = OB | Given
∠AOD = ∠COB
| Vertically Opposite Angles
∴ ∆OAD ≅ ∆OCB
| SAS Congruence Rule
∴ AD = CB | C.P.C.T.
∠ODA = ∠OBC | C.P.C.T.
∴ ∠BDA = ∠DBC
∴ AD || BC
Now, ∵ AD = CB and AD || CB
∴ Quadrilateral ABCD is a || gm.
In ∆AOB and ∆AOD,
AO = AO | Common
OB = OD | Given
∠AOB = ∠AOD
| Each = 90° (Given)
∴ ∆AOB ≅ ∆AOD
| SAS Congruence Rule
∴ AB = AD
Now, ∵ ABCD is a parallelogram and
∴ AB = AD
∴ ABCD is a rhombus.
Again, in ∆ABC and ∆BAD,
AC = BD | Given
BC = AD
| ∵ ABCD is a rhombus
AB = BA | Common
∴ ∆ABC ≅ ∆BAD
| SSS Congruence Rule
∴ ∆ABC = ∆BAD | C.P.C.T.
AD || BC
| Opp. sides of || gm ABCD and transversal AB intersects them.
∴ ∠ABC + ∠BAD = 180°
| Sum of consecutive interior angles on the same side of a transversal is 180°
∴ ∠ABC = ∠BAD = 90°
Similarly, ∠BCD = ∠ADC = 90°
∴ ABCD is a square.
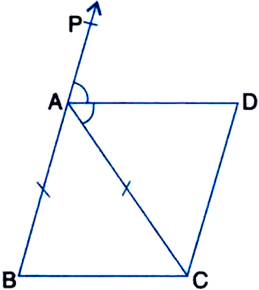
Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i) it bisects ∠C also
(ii) ABCD is a rhombus.
Given: Diagonal AC of a parallelogram ABCD bisects ∠A.
To Prove: (i) it bisects ∠C also.
(ii) ABCD is a rhombus.
Proof: (i) In ∆ADC and ∆CBA,
AD = CB
| Opp. sides of || gm ABCD
CA = CA | Common
DC = BA
| Opp. sides of || gm ABCD
∴ ∆ADC ≅ ∆CBA
| SSS Congruence Rule
∴ ∠ACD = ∠CAB | C.RC.T.
and ∠DAC = ∠BCA | C.RC.T.
But ∠CAB = ∠DAC | Given
∴ ∠ACD = ∠BCA
∴ AC bisects ∠C also.
(ii) From above,
∠ACD = ∠CAD
∴ AD = CD
| Sides opposite to equal angles of a triangle are equal
∴ AB = BC = CD = DA
| ∵ ABCD is a || gm
∴ ABCD is a rhombus.
ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Given: ABCD is a rhombus.
To Prove: (i) Diagonal AC bisects ∠A as well as ∠C.
(ii) Diagonal BD bisects ∠B as well as ∠D.
Proof: ∵ ABCD is a rhombus
∴ AD = CD
∴ ∠DAC = ∠DCA ...(1)
| Angles opposite to equal sides of a triangle are equal
Also, AD || BC
and transversal AC intersects them
∴ ∠DAC = ∠BCA ...(2)
| Alt. Int. ∠s
From (1) and (2)
∠DCA = ∠BCA
⇒ AC bisects ∠C
Similarly AC bisects ∠A.
(ii) Proceeding similarly as in (i) above, we can prove that BD bisects ∠B as well as ∠D.
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.
Given: ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C.
To Prove: (i) ABCD is a square.
(ii) diagonal BD bisects ∠B as well as ∠D.
Proof: (i) ∵ AB || DC
and transversal AC intersects them.
∴ ∠ACD = ∠CAB | Alt. Int. ∠s
But ∠CAB = ∠CAD
∴ ∠ACD = ∠CAD
∴ AD = CD
| Sides opposite to equal angles of a triangle are equal
∴ ABCD is a square.
(ii) In ∆BDA and ∆DBC,
BD = DB | Common
DA= BC
| Sides of a square ABCD
AB = DC
| Sides of a square ABCD
∴ ∆BDA ≅ ∆DBC
| SSS Congruence Rule
∴ ∠ABD = ∠CDB | C.P.C.T.
But ∠CDB = ∠CBD
| ∵ CB = CD (Sides of a square ABCD)
∴ ∠ABD = ∠CBD
∴ BD bisects ∠B.
Now, ∠ABD = ∠CBD
∠ABD = ∠ADB | ∵ AB = AD
∠CBD = ∠CDB | ∵ CB = CD
∴ ∠ADB = ∠CDB
∴ BD bisects ∠D.
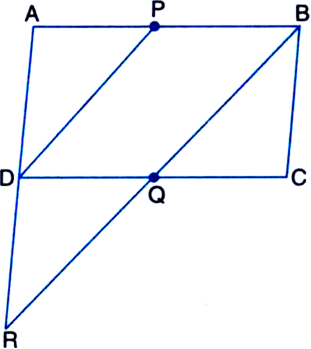
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:
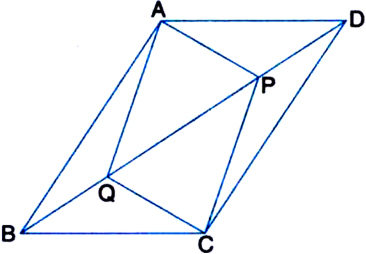
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
Given: In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ.
To Prove: (i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
Construction: Join AC to intersect BD at O.
Proof: (i) In ∆APD and ∆CQB,
∵ AD || BC
| Opposite sides of parallelogram ABCD and a transversal BD intersects them
∴ ∠ADB = ∠CBD
| Alternate interior angles
⇒ ∠ADP = ∠CBQ ...(1)
DP = BQ | Given (2)
AD = CB ...(3)
| Opposite sides of ||gm ABCD In view of (1), (2) and (3)
∆APD ≅ ∆CQB
| SAS congruence criterion
(ii) ∵ ∆APD ≅ ∆CQB
| Proved in (i) above
∴ AP = CQ | C.P.C.T.
(iii) In ∆AQB and ∆CPD,
∵ AB || CD
| Opposite sides of ||gm ABCD and a transversal BD intersects them
∴ ∠ABD = ∠CDB
| Alternate interior angles
⇒ ∠ABQ = ∠CDP
QB = PD | Given
AB = CD
| Opp. sides of || gm ABCD
∴ ∆AQB ≅ ∆CPD | SAS Congruence Rule
(iv) ∵ ∆AQB = ∆CPD
| Proved in (iii) above
∴ AQ = CP | C.P.C.T.
(v) ∵ The diagonals of a parallelogram bisect each other.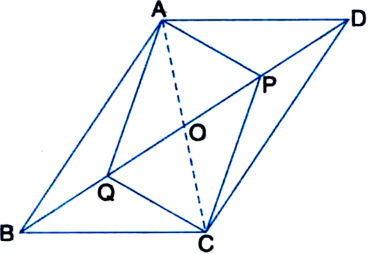
∴ OB = OD
∴ OB - BQ = OD - DP
| ∵ BQ = DP (given)
∴ OQ = OP ...(1)
Also, OA = OC ...(2)
| ∵ Diagonals of a || gm bisect each other
In view of (1) and (2), APCQ is a parallelogram.
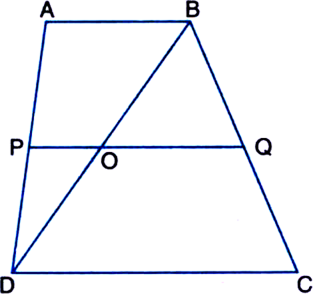
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.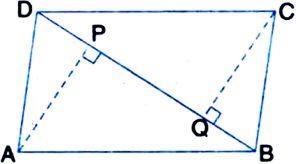
Given: ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively.
To Prove: (i) ∆APB ≅ ∆CQD
(ii) AP = CQ.
Proof: (i) In ∆APB and ∆CQD,
AB = CD
| Opp. sides of || gm ABCD
∠ABP = ∠CDQ
| ∵ AB || DC and transversal BD intersects them
∠APB = ∠CQD | Each = 90°
∆APB ≅ ∆CQD
| ∵ AAS Congruence Rule
(ii) ∵ ∆APB ≅ ∆CQD
| Proved above in (i)
∴ AP = CQ. | C.P.C.T.
In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram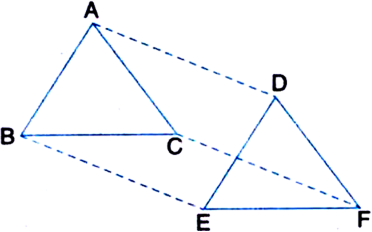
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF. [CBSE 2012
Given: In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively.
To Prove: (i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF.
Proof: (i) In quadrilateral ABED,
AB = DE and AB || DE
| Given
∴ quadrilateral ABED is a parallelogram.
| ∵ A quadrilateral is a parallelogram if a pair of opposite sides are parallel
and are of equal length
(ii) In quadrilateral BEFC,
BC = EF and BC || EF | Given
∴ quadrilateral BEFC is a parallelogram.
| ∵ A quadrilateral is a parallelogram if a pair of opposite sides are parallel
and are of equal length
(iii) ∵ ABED is a parallelogram
| Proved in (i)
∴ AD || BE and AD = BE ...(1)
| ∵ Opposite sides of a || gm
are parallel and equal
∵ BEFC is a parallelogram | Proved in (ii)
∴ BE || CF and BE = CF ...(2)
| ∵ Opposite sides of a || gm
are parallel and equal
From (1) and (2), we obtain
AD || CF and AD = CF.
(iv) In quadrilateral ACFD,
AD || CF and AD = CF
| From (iii)
∴ quadrilateral ACFD is a parallelogram.
| ∵ A quadrilateral is a parallelogram if a pair of opposite sides are parallel and are of equal length
(v) ∵ ACFD is a parallelogram
| Proved in (iv)
∴ AC || DF and AC = DF.
| In a parallelogram opposite sides are parallel and of equal length
(vi) In ∆ABC and ∆DEF,
AB = DE
| ∵ ABED is a parallelogram
BC = EF
| ∵ BEFC is a parallelogram
AC = DF | Proved in (v)
∴ ∆ABC ≅ ∆DEF.
| SSS Congruence Rule
ABCD is a trapezium in which AB || CD and AD = BC (see figure): Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC = ∆BAD
(iv) diagonal AC = diagonal BD.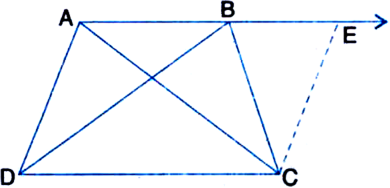
[Hint. Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
Given: ABCD is a trapezium in which AB || CD and AD = BC.
To Prove: (i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD
(iv) diagonal AC = diagonal BD. Construction: Extend AB and draw a line
through C parallel to DA intersecting AB produced at E
Proof: (i) AB || CD | Given
and AD || EC | By construction
∴ AECD is a parallelogram
| A quadrilateral is a parallelogram if a pair of opposite sides are parallel and are of
equal length
∴ AD = EC
| Opp. sides of a || gm are equal
But AD = BC | Given
∴ EC = BC
∴ ∠CBE = ∠CEB ...(1)
| Angles opposite to equal sides of a triangle are equal
∠B + ∠CBE = 180° ...(2)
| Linear Pair Axiom
∵ AD || EC | By construction
and transversal AE intersects them
∴ ∠A + ∠CEB = 180° ...(3)
| The sum of consecutive interior angles on the same side of a transversal is 180°
From (2) and (3),
∠B + ∠CBE = ∠A + ∠CEB
But ∠CBE = ∠CEB | From(1)
∴ ∠B = ∠A
or ∠A = ∠B
(ii) ∵ AB || CD
∠A + ∠D = 180°
| The sum of consecutive interior angles on a same side of a transversal is 180°
and ∠B + ∠C = 180°
∴ ∠A + ∠D = ∠B + ∠C
But ∠A = ∠B | Proved in (i)
∴ ∠D = ∠C
or ∠C = ∠D
(iii) In ∆ABC and ∆BAD,
AB = BA | Common
BC = AD | Given
∠BC = ∠BAD | From (i)
∴ ∆ABC ≅ ∆BAD.
| SAS Congruence Rule
(iv) ∵ ∆ABC ≅ ∆BAD
| From (iii) above
∴ AC = BD. | C.P.C.T.
In a parallelogram, show that the angle bisectors of two adjacent angles intersect at right angles.
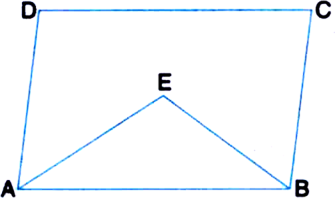
To Prove: ∠AEB = 90°
Proof: ∵ AD || BC
| Opposite sides of ||gm and transversal AB intersects them
∴ ∠DAB + ∠CBA = 180°
| ∵ Sum of consecutive interior angles on the same side of a transversal is 180°
⇒ 2∠EAB + 2∠EBA = 180°
| ∵ AE and BE are the bisectors of ∠DAB and ∠CBA respectively.
⇒ ∠EAB + ∠EBA = 90° ...(1)
In ∆EAB,
∠EAB + ∠EBA + ∠AEB = 180°
| ∵ The sum of the three angles of a triangle is 180°
⇒ 90° + ∠AEB = 180° | From (1)
⇒ ∠AEB = 90°.
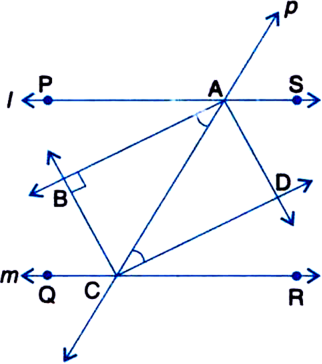
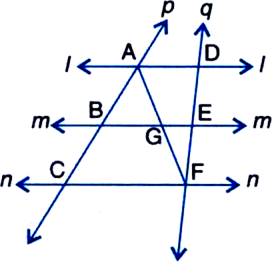
AB and CD are two parallel lines and a transversal I intersects AB at X and CD at Y. Prove that the bisectors of the interior angles form a rectangle.
Given: AB and CD are two parallel lines and a transversal I intersects AB at X and CD at Y.
To Prove: The bisectors of the interior angles form a rectangle.
Proof: ∵ AB || CD and EF intersects them
∴ ∠BXY = ∠CYX
| Alternate interior ∠s![]()
| Halves of equals are equal![]()
But these angles form a pair of equal alternate angles for lines XQ and SY and a transversal XY.
∴ XQ || SY ...(1)
Similarly, we can prove that
SX || YQ ...(2)
In view of (1) and (2),
SYQX is a parallelogram
| ∵ A quadrilateral is a parallelogram if both pairs of its opposite sides are parallel
Now, ∠BXY + ∠DYX = 180°
| Consecutive interior ∠s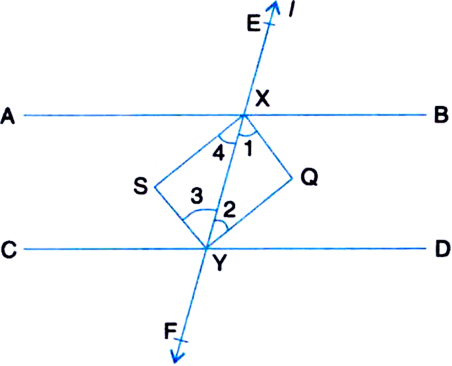
![]()
⇒ ∠1 + ∠2 = 90°
But ∠1 + ∠2 + ∠XQY = 180°
| Angle sum property of a ∆
⇒ 90° + ∠XQY = 180°
⇒ ∠XQY = 90°
⇒ ∠YSX = 90°
| Opposite ∠s of a ||gm are equal
and ∠SXQ = 90°
| ∵ Consecutive interior angles on the same side of a transversal are supplementary
Now, ∠SXQ = 90°
⇒ ∠SYQ = 90°
| Opposite ∠s of a ||gm are equal
Thus each angle of the parallelogram SYQX is 90°. Hence parallelogram SYQX is a
rectangle.
ABCD is a parallelogram and line segments AX, CY bisect the angles A and C respectively. Show that AX || CY.
Given: ABCD is a parallelogram and line segments AX, CY bisect the angles A and C respectively.
To Prove: AX || CY.
Proof: ∵ ABCD is a parallelogram.
∴ ∠A = ∠C | Opposite ∠s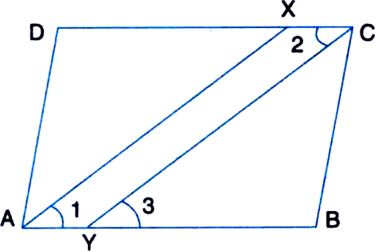
![]()
| ∵ Halves of equals are equal
⇒ ∠1 = ∠2 ....(1)
| ∵ AX is the bisector of ∠A and CY is the bisector of ∠C
Now, AB || DC and CY intersects them
∴ ∠2 = ∠3 ...(2)
| Alternate interior ∠s
From (1) and (2), we get
∠1 = ∠3
But these form a pair of equal corresponding angles
∴ AX || CY.
If a diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle and then the two diagonals are perpendicular to each other.
Given: ABCD is a ||gm. Diagonal AC bisects ∠A.
To Prove: (i) AC bisects ∠C
(ii) AC ⊥ BD.
Proof: (i) ∵ AB || DC and AC intersects them
∴ ∠1 = ∠4
| Alternate Interior ∠s
Similarly, ∠2 = ∠3
| Alternate Interior ∠s
But ∠1 = ∠2
∴ ∠3 = ∠4
⇒ AC bisects ∠C.
(ii) In ∆ADC,
∠2 = ∠4
∴ AD = CD
| Sides opposite to equal angles of a triangle are equal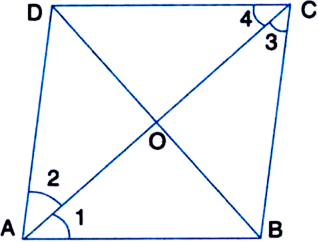
In ∆AOD and ∆COD,
OA = OC | ∵ Diagonals
of a ||gm bisect each other
OD = OD | Common side
AD = CD | Proved above
∴ ∆AOD ≅ ∆COD
| SSS Congruence Axiom
∴ ∠AOD = ∠COD | C.P.C.T.
But ∠AOD + ∠COD = 180°
| Linear Pair Axiom
⇒ 2∠AOD = 180°
| ∵ ∠AOD = ∠COD
⇒ ∠AOD = 90°
⇒ AC ⊥ BD.
Given ∆ABC, lines are drawn through A, B and C parallel respectively to the sides
BC, CA and AB forming ∆PQR. Show that BC = ![]()
To Prove: BC=
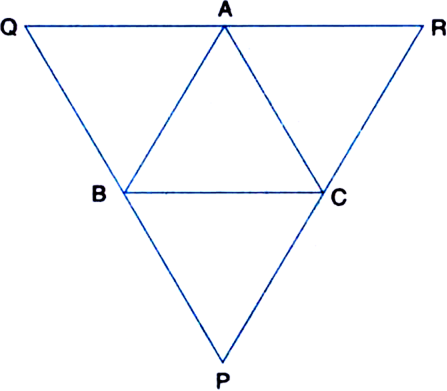
Proof: ∵ AQ || CB and AC || QB
∴ AQBC is a parallelogram
∴ BC = QA ...(1)
| Opposite sides of a ||gm
∵ AR || BC and AB || RC
∴ ARCB is a parallelogram
∴ BC = AR ...(2)
| Opposite sides of a ||gm
From (1) and (2),
From (1) and (3), BC =
Sponsor Area
“A diagonal of a parallelogram divides it into two congruent triangles.” Prove it.
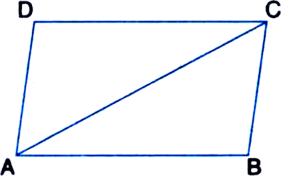
To Prove: ∆ABC ≅ ∆CDA
Proof: BC || DA
| Opposite sides of a parallelogram are parallel
and AC is a transversal
∴ ∠BCA = ∠DAC ...(1)
| Pair of alternate interior angles
Also, AB || DC
Opposite sides of a parallelogram are parallel
and AC is a transversal
∴ ∠BAC = ∠DCA ...(2)
| Pair of alternate interior angles
AC = CA ...(3) | Common
In view of (1), (2) and (3),
∆ABC ≅ ∆CDA
| ASA congruence criterion
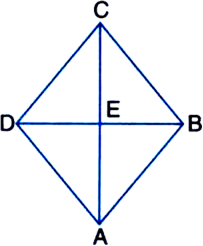
Show that the diagonals of a square are equal and perpendicular to each other.
Given: ABCD is a square. AC and BD are its diagonals.
To Prove: AC = BD; AC ⊥ BD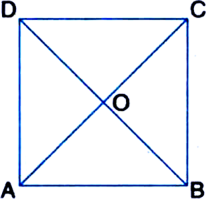
Proof: In ∆ABC and ∆BAD,
AB = BA | Common
∠ABC = ∠BAD | Each = 90°
BC = AD
| Sides of a square are equal
∴ ∆ABC ≅ ∆BAD
| SAS congruence criterion
∴ AC = BD | CPCT
Again, in ∆AOB and ∆AOD,
AO = AO | Common
AB = AD
| Sides of a square are equal
OB = OD
| A square is a parallelogram and the diagonals of a parallelogram bisect each other
∴ ∆AOB ≅ ∆AOD
| SSS congruence criterion
∴ ∠AOB = ∠AOD | CPCT
But ∠AOB + ∠AOD = 180°
| Linear Pair Axiom
∴ ∠AOB = ∠AOD = 90°
⇒ AO ⊥ BD
⇒ AC ⊥ BD.
ABCD is a trapezium in which AB || CD and AD = BC. Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD.
Given: ABCD is a trapezium in which AB || CD and AD = BC
To Prove:
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD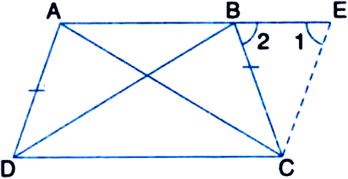
Construction: Through C, draw CE || DA to intersect AB produced at E.
Proof:
(i) ∵ AB || CD | Given
and AD || CE | by construction
∴ AECD is a parallelogram
| A quadrilateral is a parallelogram if both the pairs of opposite sides are parallel
∴ AD = EC
| Opposite sides of a parallelogram are equal
But AD = BC | Given
∴ BC = EC
∴ ∠1 = ∠2
| Angles opposite to equal sides of a triangle are equal
∠B + ∠2 = 180° ...(1)
| Linear Pair Axiom
∵ AD || EC | by construction
and AE intersects them
∴ ∠A + ∠1 = 180° ...(2)
| Sum of the consecutive interior angles on the same side of a transversal is 180°
From (1) and (2),
∠B + ∠2 = ∠A + ∠1
But ∠1 = ∠2 | Proved above
∴ ∠B = ∠A
⇒ ∠A = ∠B
(ii) ∵ AB || DC | Given
and AD is a transversal
∴∠A + ∠D = 180° ...(3)
| Sum of the consecutive interior angles on the same side of a transversal is 180°
∵ AB || DC | Given
and BC is a transversal.
∴ ∠B + ∠C = 180° ...(4)
| Sum of the consecutive interior angles on the same side of a transversal is 180°
From (3) and (4),
∠A + ∠D = ∠B + ∠C
But ∠A = ∠B | Proved in (i
∴ ∠D = ∠C
⇒ ∠C = ∠D.
(iii) In ∆ABC and ∆BAD,
AB = BA | Common
BC = AD | Given
∠ABC = ∠BAD | Proved in (i)
∴ ∆ABC ≅ ∆BAD
| SAS congruence criterion
Prove that each angle of a rectangle is a right angle.
Given: ABCD is a rectangle with
∠A = 90°.
To Prove: ∠A = ∠B = ∠C = ∠D = 90°
Proof: ∵ ABCD is a rectangle
∴ ABCD is a parallelogram
∴ AD || BC
| Opposite sides of a parallelogram are
parallel
and transversal AB intersects them
∴ ∠A + ∠B = 180°
| Sum of the consecutive interior angles on the same side of a transversal is 180°
⇒ 90° + ∠B = 180° | ∵ ∠A = 90° (given)
⇒ ∠B = 90°
Similarly, we can show that
∠C = 90° and ∠D = 90°
Hence, ∠A = ∠B = ∠C = ∠D = 90°.
In a quadrilateral ABCD, the line segments bisecting ∠C and ∠D meet at E.
Prove that ∠A + ∠B = 2 ∠CED
Given: In a quadrilateral ABCD, the line segments bisecting ∠C and ∠D meet at E.]
To Prove: ∠A + ∠B = 2∠CED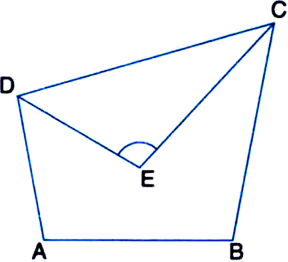
Proof: In quadrilateral ABCD,
∠A + ∠B + ∠C + ∠D = 360° ...(1)
| Angle sum property of a quadrilateral
In ∆CED,
∠CED + ∠EDC + ∠ECD = 180°
| Angle sum property of a triangle![]()
⇒ 2 ∠CED + ∠D + ∠C = 360° ...(2)
From (1) and (2),
2 ∠CED + ∠D + ∠C = ∠A + ∠B + ∠C + ∠D
⇒ 2 ∠CED = ∠A + ∠B
⇒ ∠A + ∠B = 2 ∠CED
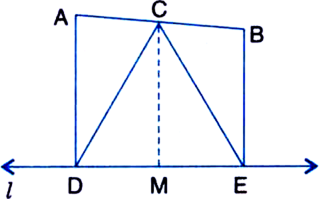
ABC is an isosceles triangle in which AB = AC. AD bisects ∠PAC and CD || AB. Show that
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram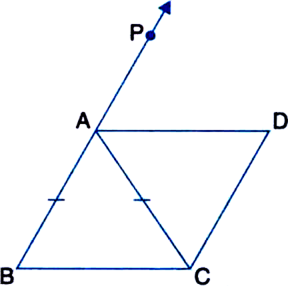
Given: ABC is an isosceles triangle in which AB = AC. AD bisects ∠PAC and CD || AB.
To Prove:
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram.
Proof:
(i) In ∆ABC,
∵ AB = AC
∴ ∠B = ∠C ...(1)
| Angles opposite to equal sides of a triangle are equal
Also, Ext. ∠PAC = ∠B + ∠C
| An exterior angle of a triangle is equal to the sum of two interior opposite angles
⇒ ∠PAC = ∠C + ∠C | From (1)
⇒ 2 ∠CAD = 2 ∠C | ∵ AD bisects ∠PAC
⇒ ∠CAD = ∠C
⇒ ∠DAC = ∠BCA
(ii) But these angles form a pair of equal alternate interior angles
∴ AD || BC
Also, CD || AB
∴ ABCD is a parallelogram
| A quadrilateral is a parallelogram if its both the pairs of opposite sides are parallel.
Show that the diagonals of a rhombus are perpendicular to each other.
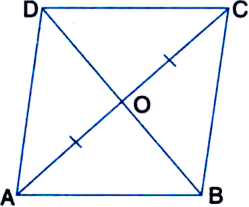
Solution not provided.
Show that the bisectors of angles of a parallelogram form a rectangle.
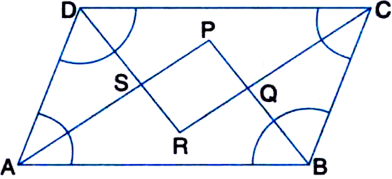
Solution not provided.
If an angle of a parallelogram in two-third of its adjacent angle then find the measure of all the angles.
Solution not provided.
The angles A, B, C and D of a quadrilateral have measures in the ratio 2 : 4 : 5 : 7. Find the measures of these angles. What type of quadrilateral is it? Give reasons.
Solution not provided.
Ans. 40°, 80°, 100°, 140°; Trapezium
If the diagonals of a quadrilateral bisect each other, prove that it is a parallelogram.
Solution not provided.
In a parallelogram PQRS, if ∠QRS = 2x, ∠PQS = 4x and ∠PSQ = 4x, find the angles of the parallelogram.
Solution not provided.
Ans. 36°, 144°, 36°, 144°
In the figure, ABCD is a parallelogram in which AB is produced to E so that AB = BE
(a) Prove that ED bisects BC
(b) If AD = 10 cm, find OB.
Solution not provided.
Ans. 5 cm
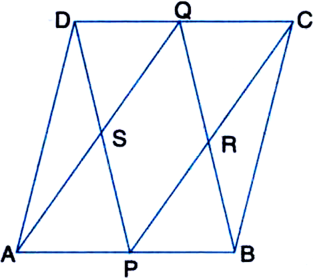
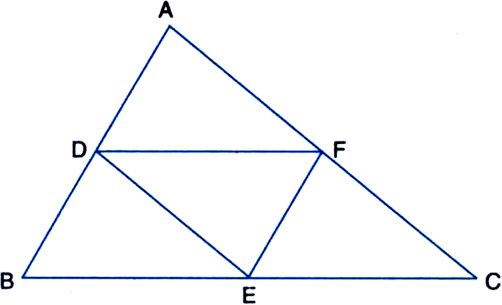
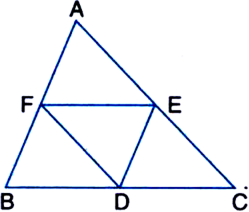
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see figure). AC is a diagonal. Show that:
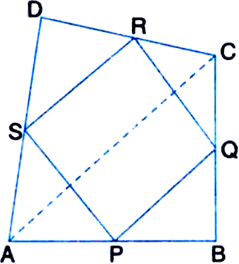

(ii) PQ = SR
(iii) PQRS is a parallelogram.
To Prove:
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Proof : (i) In
| MId-point therorem
(ii) In
| Mid-point theorem
But from (i)
(iii) PQ || AC | From (ii)
SR || AC | From (i)
∴ PQ || SR
| Two lines parallel to the same line are parallel to each other
Also, PQ = SR | From (ii)
∴ PQRS is a parallelogram.
| A quadrilateral is a parallelogram if a pair of opposite sides are parallel and are of equal length
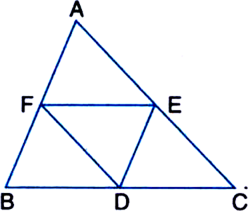
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Given: ABCD is a rhombus. P, Q, R, S are the mid-points of AB, BC, CD, DA respectively. PQ, QR, RS and SP are joined.
To Prove: PQRS is a rectangle.
Construction: Join AC and BD.
Proof: In triangles RDS and PBQ,
DS = QB
| Halves of opposite sides of || gm ABCD which are equal
DR = PB
| Halves of opposite sides of || gm ABCD which are equal
∠SDR = ∠QBP
| Opposite ∠s of ||gm ABCD which are equal
∴ ∆RDS = ∆PBQ
| SAS Congruence Axiom
∴ SR = PQ | C.P.C.T.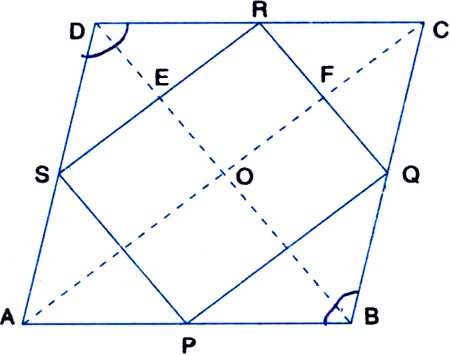
In triangles RCQ and PAS,
RC = AP
| Halves of opposite sides of || gm ABCD which are equal
CQ = AS
Halves of opposite sides of || gm ABCD which are equal
∠RCQ = ∠PAS
Opposite ∠s of || gm ABCD which are equal
∴ ∆RCQ ≅ ∆PAS
| SAS Congruence Axiom
∴ RQ = SP | C.P.C.T.
∴ In PQRS,
SR = PQ and RQ = SP
∴ PQRS is a parallelogram,
In ∆CDB,
∵ R and Q are the mid-points of DC and CB respectively.
∴ RQ || DB ⇒ RF || EO.
Similarly, RE || FO
∴ OFRE is a || gm
∴ ∠R = ∠EOF = 90°
| ∵ Opposite ∠s of a || gm are equal and diagonals of a rhombus intersect at 90°
Thus PQRS is a rectangle.
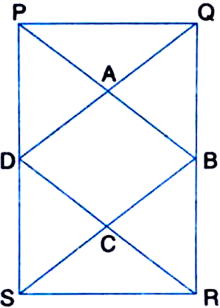
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
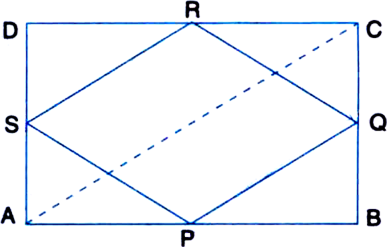
To Prove: Quadrilateral PQRS is a rhombus.
Construction: Join AC.
Proof: In ∆ABC,![]() P and Q are the mid-points of AB and BC respectively.
P and Q are the mid-points of AB and BC respectively.![]()
In ![]()
![]() S and R are the mid-points of AD and DC respectively.
S and R are the mid-points of AD and DC respectively.![]()
From (1) and (2),![]()
![]() Quardrilateral PQRS is a parallelogram ....(3_
Quardrilateral PQRS is a parallelogram ....(3_
In rectangle ABCD,
AD = BC | Opposite sides![]()
| Halves of equals are equal![]() AS = BQ
AS = BQ
In ![]()
AP = BP
| ∵ P is the mid-point of AB
AS = BQ | Proved above
∠PAS = ∠PBQ | Each = 90°
∴ ∆APS ≅ ∆BPQ
| SAS Congruence Axiom
∴ PS = PQ ...(4) | C.P.C.T.
In view of (3) and (4), PQRS is a rhombus.
Sponsor Area
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see figure). Show that F is the midpoint of BC.
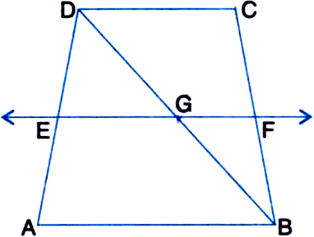
Given: ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F.
To Prove: F is the mid-point of BC.
Proof: Let DB intersect EF at G.
In ∆DAB,
∵ E is the mid-point of DA and EG || AB
∴ G is the mid-point of D
| By converse of mid-point theorem
Again, in ∆BDC,
∵ G is the mid-point of BD and GF || AB || DC
∴ F is the mid-point of BC.
| By converse of mid-point theorem
In a parallelogram ABCD, E and Fare the mid-points of sides AB and CD respectively. (see figure). Show that the line segments AF and EC trisect the diagonal BD.
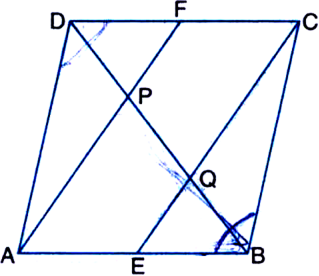
Given: In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively.
To Prove: Line segments AF and EC trisect the diagonal BD.
Proof: ![]()
| Opposite sides of ![]() gm ABCD
gm ABCD![]() AE
AE ![]() FC .....(1)
FC .....(1)![]() AB = DC
AB = DC
| Opposite sides of ![]() gm ABCD
gm ABCD![]()
| Halves of equals are equal![]() AE = CF ....(2)
AE = CF ....(2)
In view of (1) and (2),
AECF is a parallelogram
| A quadrilateral is a parallelogram if a pair of opposite sides are parallel and are of equal length
∴ EC || AF ...(3)
| Opposite sides of || gm AECF
In ∆DQC,
∵ F is the mid-point of DC
and FP || CQ | ∵ EC || AF
∴ P is the mid-point of DQ
| By converse of mid-point theorem
⇒ DP = PQ ...(4)
Similarly, in ∆BAP,
BQ = PQ ...(5)
From (4) and (5), we obtain
DP = PQ = BQ
⇒ Line segments AF and EC trisect the diagonal BD.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Given: ABCD is a quadrilateral. P, Q, R and S are the mid-points of the sides DC, CB, BA and AD respectively.
To Prove: PR and QS bisect each other.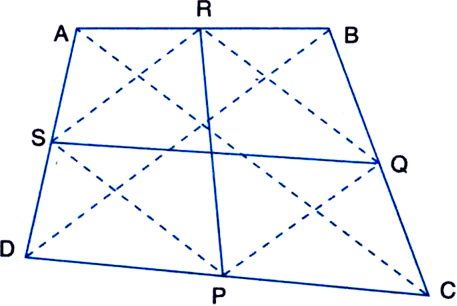
Construction: Join PQ, QR, RS, SP, AC and
BD.
Proof: In ∆ABC,
∵ R and Q are the mid-points of AB and BC respectively.![]()
Similarly, we can show that![]()
Thus a pair of opposite sides of a quadrilateral PQRS are parallel and equal.
PQRS is a parallelogram.
Since the diagonals of a parallelogram bisect each other.
∴ PR and QS bisect each other.
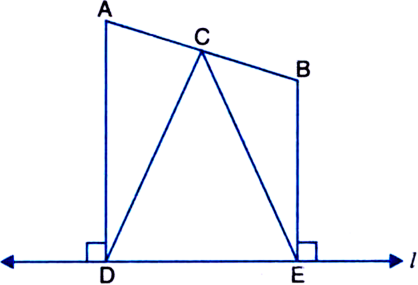
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that:
(i) D is the mid-point of AC (ii) MD ⊥ AC (iii) ![]()
Given: ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D.
To Prove: (i) D is the mid-point of AC.
(ii) MD ⊥ AC
(iii) ![]()
Proof: (i) In ∆ACB,
∵ M is the mid-point of AB and MD || BC
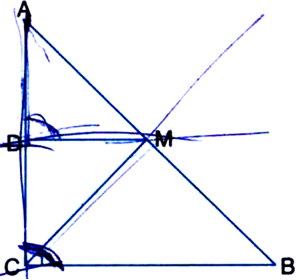
∴ D is the mid-point of AC.
| By converse of mid-point theorem
(ii) ∵ MD || BC and AC intersects them
∴ ∠ADM = ∠ACB
| Corresponding angles
But ∠ACB = 90° | Given
∴ ∠ADM = 90° ⇒ MD ⊥ AC
(iii) Now, ∠ADM + ∠CDM = 180°
| Linear Pair Axiom
∴ ∠ADM = ∠CDM = 90°
In ∆ADM and ∆CDM,
AD = CD
| ∵ D is the mid-point of AC
∠ADM = ∠CDM | Each = 90°
DM = DM | Common
∴ ∆ADM ≅ ∆CDM
| SAS Congruence Rule
∴ MA = MC | C.P.C.T.
But M is the mid-point of AB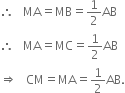
In triangle ABC, points M and N on sides AB and AC respectively are taken so that
 Prove that MN =
Prove that MN = 
To Prove:
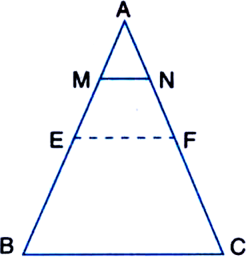
Construction: Join EF where E and F are the middle points of AB and AC respectively.
Proof: Y E is the mid-point of AB and F is the mid-point of AC.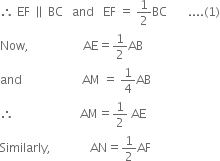
![]() M and N are the mid-points of AE and AF respectively.
M and N are the mid-points of AE and AF respectively.![]()
| From (1)
![]()
In triangle ABC, points M and N on sides AB and AC respectively are taken so that

To prove:
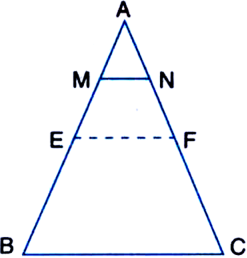
Construction: Join EF where E and F are the middle points of AB and AC respectively.
Proof: Y E is the mid-point of AB and F is the mid-point of AC.
| From (1)
ABCD is a rhombus and AB is produced to E and F such that AE = AB = BF. Prove that ED and FC are perpendicular to each other.
Given: ABCD is a rhombus and AB is produced to E and F such that AE = AB = BF.
To Prove: ED ⊥ FC.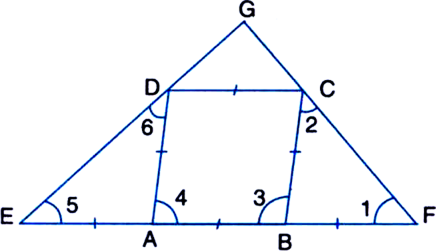
Proof: AB = BF | By construction
AB = BC
| ∵ ABCD is a rhombus
∴ BC = BF
∴ ∠1 = ∠2 ...(1)
| Angles opposite to equal sides of a ∆ are equal
In ∆BCF,
Ext. ∠3 = ∠1 + ∠2 = ∠1 + ∠1
| From(1)
= 2 ∠1 ...(2)
AB = AE | By construction
AB = AD
| ∵ ABCD is a rhombus
∴ AD = AE
∴ ∠5 = ∠6 ...(3)
| Angles opposite to equal sides of a ∆ are equal
In ∆ADE,
Ext. ∠4 = ∠5 + ∠6 = ∠5 + ∠5
| From (3)
= 2 ∠5 ...(4)
∵ AD || BC
and transversal AB intersects them
∴ ∠3 + ∠4 = 180°
| ∵ Consecutive interior angles on the same side of a transversal are supplementary
⇒ 2∠1 + 2∠5 = 180° | From (2) and (4)
⇒ ∠1 + ∠5 = 90° ...(5)
In ∆GEF,
∠1 + ∠5 + ∠EGF = 180°
| ∵ The sum of the three angles of a ∆ is 180°
⇒ 90° + ∠EGF = 180° | From (5)
⇒ ∠EGF = 90°
⇒ EG ⊥ GF
⇒ ED ≁ FC.
In ∆ABC, AD is the median through A and E is the mid-point of AD. BE is produced to meet AC in F. Prove that 
To Prove: AF=
Construction: Draw DG || EF to intersect AC in G.
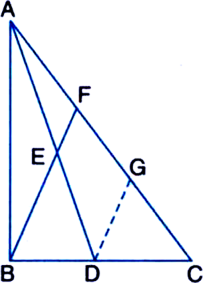
Proof: ∵ EF || DG | by construction
and AE = ED
| ∵ E is the mid-point of AD
∴ AF = FG ...(1)
| A line drawn through the mid-point of a side of a triangle parallel to another side bisects the third side
Again,
DG || EF | by construction
and CD = DB
| ∵ D is the mid-point of
∴ BC FG = GC ...(2)
| A line drawn through the mid-point of a side of a triangle parallel to another side bisects the third side
From (1) and (2),
AF = FG = GC
Now, AF + FG + GC = AC
⇒ AF + AF + AF = AC
| From (1) and (2)
⇒ 3 AF = AC
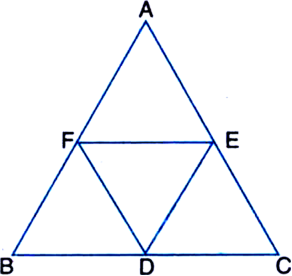
D, E, F are respectively the midpoints of the sides BC, CA and AB of a triangle ABC. Show that:
(i) BDEF is a parallelogram
(ii) DFEC is a parallelogram.
Given: D, E, F are respectively the midpoints of the sides BC. CA and AB of a triangle ABC. To Prove:
(i) BDEF is a parallelogram
(ii) DFEC is a parallelogram.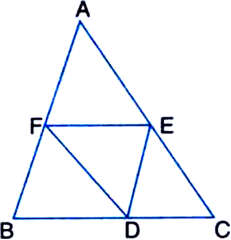
Proof:
(i) In ∆ABC,
∵ F is the mid-point of AB and E is the mid-point of AC
∴ FE || BC | By mid-point theorem
⇒ FE || BD ...(1)
Again, In ∆ABC,
∵ D is the mid-point of BC and E is the midpoint of AC.
∴ DE || BA | By mid-point theorem
In the figure ABCD is a parallelogram and E is the mid-point of side BC. DE and AB on producing meet at F. Prove that AF = 2AB.
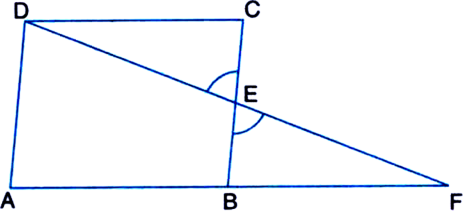
Given: ABCD is a parallelogram and E is the mid-point of side BC. DE and AB on producing meet at F.
To Prove: AF = 2AB
Proof: In ∆FAD,
∵ E is the mid-point of BC | Given
and EB || DA
| Opposite sides of a parallelogram are parallel
∴ B is the mid-point of AF | by converse of
mid-point theorem![]()
ABCD is a trapezium in which side AB is parallel to the side DC and E is the mid-point of side AD (see figure). If F is a point on the side BC such that the segment EF is parallel to the side DC, prove that F is the mid-point of BC and EF =  (AB + DC).
(AB + DC).
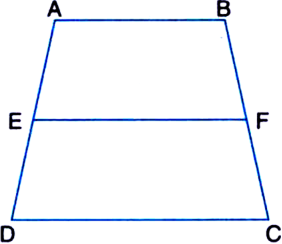
Given: ABCD is a trapezium in which side AB is parallel to the side DC and E is the mid-point of side AD. F is a point on the side BC such that the segment EF is parallel to the side DC.
To Prove: F is the mid-point of BC
and ![]()
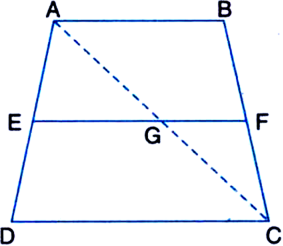
Construction: Join AC to intersect EF at G.
Proof:
(i) In ∆ADC,
∵ E is the mid-point of AD and
EG || DC | ∵ EF || DC
∴ G is the mid-point of AC
| by converse of mid-point theorem Again, In ∆CAB,
∵ G is the mid-point of AC | proved above
and GF || DC | ∵ EF || DC
∴ F is the mid-point of BC | by converse of
mid-point theorem
(ii) We shall prove that the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and half of it.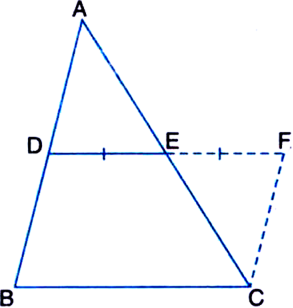
Let ABC be a triangle in which D and E are the mid-points of the sides AB and AC respectively.
We produce DE to F such that DE = EF and join FC.
In ∆AED and ∆CEF,
AE = CE
| ∵ E is the mid-point of AC
∠AED = ∠CEF
| Vertically opposite angles
ED = EF | by construction
∴ ∆AED ≅ ∆CEF
| SAS congruence rule
∴ AD = CF |CPCT
and ∠ADE = ∠CFE | CPCT
Now, ∵ D is the mid-point of AB
∴ AD = DB
But AD = CF | Proved above
∴ DB = CF ...(1)
Again, ∵ DF intersects AD and FC such that
∠ADE = ∠CFE | Proved above
But these angles form a pair of equal alternate interior angles
∴ AD || FC
⇒ DB || FC ...(2)
In view of (1) and (2),
DBCF is a parallelogram
| A quadrilateral is a parallelogram if one pair of its opposite sides is parallel and equal
∴ DF = BC
| Opposite sides of a parallelogram are equal
⇒ 2DE = BC | by construction![]()
Also, ∵ DBCF is a parallelogram
∴ DF || BC
| Opposite sides of a parallelogram are parallel
⇒ DE || BC
(iii) Using this result in ∆ADC,![]()
| ∵ E is the mid-point of AD and G is the mid-point of AC
and in ∆CAB,![]()
| ∵ G is the mid-point of AC and F is the mid-point of BC
Adding (3) and (4), we get
Also, EG || DC
⇒ EF || DC
ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that  AC (see figure). If PQ produced meets BC at R, prove that R is the mid-point of BC.
AC (see figure). If PQ produced meets BC at R, prove that R is the mid-point of BC.
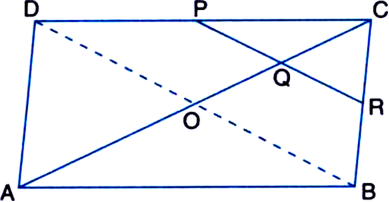
Given: ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that
AC. PQ produced meets BC at R.
To Prove: R is the mid-point of BC.
Construction: Join BD to intersect AC at O.
Proof: ∵ ABCD is a parallelogram and the diagonals of a parallelogram bisect each that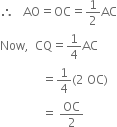
![]() Q is the mid-point of CO
Q is the mid-point of CO
In ∆CDO,
∵ P is the mid-point of DC and Q is the midpoint of CO
∴ PQ || DO | by mid-point theorem
⇒ PR || DB
⇒ QR || OB
Now, in ∆COB,
∵ Q is the mid-point of CO and QR || OB
∴ R is the mid-point of BC
| by converse of mid-point theorem
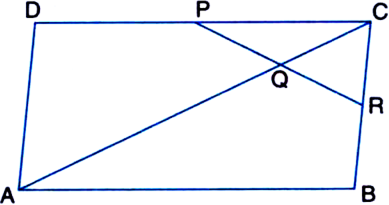
Prove that the line segment joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides.
Given: ABCD is a trapezium. P and Q are the mid-points of the diagonals AC and BD respectively.
To Prove: PQ || AB
Construction: Join DP and produce so as to meet AB in R.
Proof: In ∆APR and ∆CPD,
∠PAR = ∠PCD
| Alternate interior angels [∵ AB || DC and a transversal AC intersects them]
∠APR = ∠CPD
| Vertically opposite angles
AP = CP | Common
∴ ∆APR ≅ ∆CPD
| ASA congruence rule
∴ PR = PD | CPCT
Now, in ∆DRB,
∵ P is the mid-point of DR | Proved above and Q is the mid-point of BD |Given
∴ PQ || AB
Line segment joining the mid-points of any two sides of a triangle is parallel to the third side
But AB || DC
∴ PQ || AB || DC
In ∆ABC, D, E and F are mid-points of sides AB, BC and CA. If AB = 6 cm, BC = 7.2 cm and AC = 7.8 cm, find the perimeter of ∆DEF.
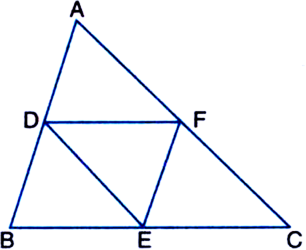
Solution not provided.
Ans. 10.5 cm
Which of the following is false?
-
a square is a rectangle
-
a square is a rhombus
-
a parallelogram is a trapezium
-
a kite is a parallelogram.
D.
a kite is a parallelogram.
Which of the following is not true?
-
a rectangle is not a square
-
a rhombus is not a square
-
a trapezium is a parallelogram
-
a kite is not a parallelogram.
C.
a trapezium is a parallelogram
Which of the following is true?
-
A diagonal of a parallelogram divides it into two congruent triangles
-
In a parallelogram, opposite angles may not be equal
-
In a parallelogram, opposite sides may be unequal
-
In a parallelogram, the diagonals do not bisect each other.
A.
A diagonal of a parallelogram divides it into two congruent triangles
Which of the following is false?
-
If each pair of opposite sides of a quadrilateral is equal, then the quadrilateral is a parallelogram
-
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram
-
If the sum of the consecutive interior angles of a quadrilateral is 90°, then the quadrilateral is a parallelogram.
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram
D.
If the sum of the consecutive interior angles of a quadrilateral is 90°, then the quadrilateral is a parallelogram.Sponsor Area
Choose the correct statement:
-
Diagonals of a rectangle are perpendicular to each other
-
Diagonals of a rhombus are perpendicular to each other
-
A kite is a parallelogram whose adjacent sides are equal
-
Diagonals of a trapezium are always equal
B.
Diagonals of a rhombus are perpendicular to each otherP and Q are the points of trisection of the diagonal AC of a parallelogram ABCD.
Prove that BQ || DP and BD bisects PQ.
Solution not provided.
ABCD is a parallelogram. P and Q are points on DC and AB respectively, such that ∠DAP = ∠BCQ. Show that AQCP is a parallelogram.

Solution not provided.
O is a point inside a rhombus ABCD such that BO = DO. Prove that AO and CO are in the same straight line.
Solution not provided.
ABCD is a parallelogram. If E is the mid-point of BC and AE is the bisector of ∠A, prove that
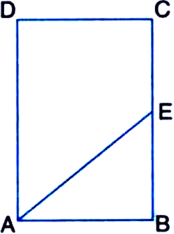
Solution not provided.
The angles of a quadrilateral are in the ratio 3:5:9:13. Find all the angles of the quadrilateral.
Solution not provided.
Ans. 36°, 60°, 108°, 156°
Mock Test Series
Sponsor Area
Sponsor Area