+91-8076753736[email protected]
logo
logo
-->

Circles

Question
CBSEENMA9002763
Wired Faculty App

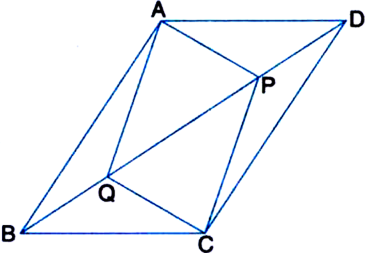
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.

Solution

Given: ABCD is a rhombus. P, Q, R, S are the mid-points of AB, BC, CD, DA respectively. PQ, QR, RS and SP are joined.
To Prove: PQRS is a rectangle.
Construction: Join AC and BD.
Proof: In triangles RDS and PBQ,
DS = QB
| Halves of opposite sides of || gm ABCD which are equal
DR = PB
| Halves of opposite sides of || gm ABCD which are equal
∠SDR = ∠QBP
| Opposite ∠s of ||gm ABCD which are equal
∴ ∆RDS = ∆PBQ
| SAS Congruence Axiom
∴ SR = PQ    | C.P.C.T.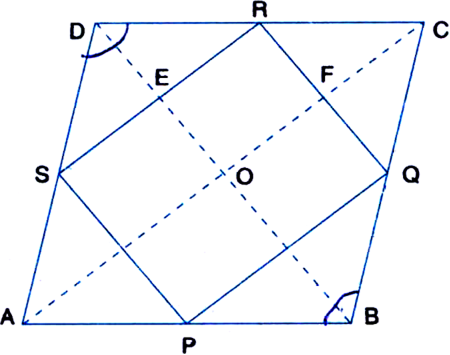

In triangles RCQ and PAS,
RC = AP
| Halves of opposite sides of || gm ABCD which are equal
CQ = AS
Halves of opposite sides of || gm ABCD which are equal
∠RCQ = ∠PAS
Opposite ∠s of || gm ABCD which are equal
∴ ∆RCQ ≅ ∆PAS
| SAS Congruence Axiom
∴ RQ = SP    | C.P.C.T.
∴ In PQRS,
SR = PQ and RQ = SP
∴ PQRS is a parallelogram,
In ∆CDB,
∵ R and Q are the mid-points of DC and CB respectively.
∴ RQ || DB ⇒ RF || EO.
Similarly, RE || FO
∴ OFRE is a || gm
∴ ∠R = ∠EOF = 90°
| ∵ Opposite ∠s of a || gm are equal and diagonals of a rhombus intersect at 90°
Thus PQRS is a rectangle.

Some More Questions From Circles Chapter

 Show that the diagonals of a square are equal and bisect each other at right angles.

Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i)    it bisects ∠C also
(ii)    ABCD is a rhombus.

ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:

(i)    ∆APD ≅ ∆CQB
(ii)   AP = CQ
(iii)  ∆AQB ≅ ∆CPD
(iv)  AQ = CP
(v)   APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.

In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i)     quadrilateral ABED is a parallelogram
(ii)    quadrilateral BEFC is a parallelogram
(iii)   AD || CF and AD = CF
(iv)   quadrilateral ACFD is a parallelogram



(v)     AC = DF
(vi)    ∆ABC ≅ ∆DEF. [CBSE 2012

ABCD is a trapezium in which AB || CD and AD = BC (see figure): Show that
(i)      ∠A = ∠B
(ii)    ∠C = ∠D
(iii)    ∆ABC = ∆BAD
(iv)    diagonal AC = diagonal BD.



[Hint. Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]

In a parallelogram, show that the angle bisectors of two adjacent angles intersect at right angles.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation