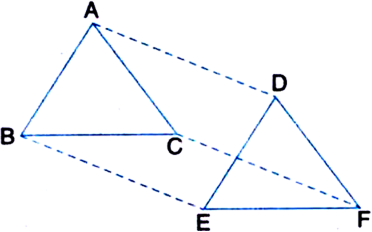
ABCD is a rhombus and AB is produced to E and F such that AE = AB = BF. Prove that ED and FC are perpendicular to each other.

Given: ABCD is a rhombus and AB is produced to E and F such that AE = AB = BF.
To Prove: ED ⊥ FC.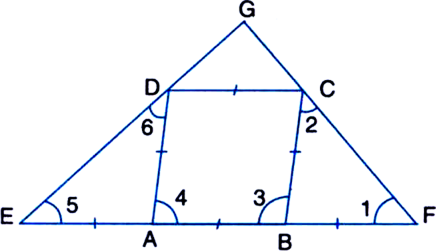

Proof: AB = BF | By construction
AB = BC
| ∵ ABCD is a rhombus
∴ BC = BF
∴ ∠1 = ∠2    ...(1)
| Angles opposite to equal sides of a ∆ are equal
In ∆BCF,
Ext. ∠3 = ∠1 + ∠2 = ∠1 + ∠1
| From(1)
= 2 ∠1    ...(2)
AB = AE    | By construction
AB = AD
| ∵ ABCD is a rhombus
∴ AD = AE
∴ ∠5 = ∠6    ...(3)
| Angles opposite to equal sides of a ∆ are equal
In ∆ADE,
Ext. ∠4 = ∠5 + ∠6 = ∠5 + ∠5
| From (3)
= 2 ∠5    ...(4)
∵ AD || BC
and transversal AB intersects them
∴ ∠3 + ∠4 = 180°
| ∵ Consecutive interior angles on the same side of a transversal are supplementary
⇒ 2∠1 + 2∠5 = 180° | From (2) and (4)
⇒ ∠1 + ∠5 = 90°    ...(5)
In ∆GEF,
∠1 + ∠5 + ∠EGF = 180°
| ∵ The sum of the three angles of a ∆ is 180°
⇒ 90° + ∠EGF = 180°    | From (5)
⇒    ∠EGF = 90°
⇒    EG ⊥ GF
⇒    ED ≁ FC.