Question
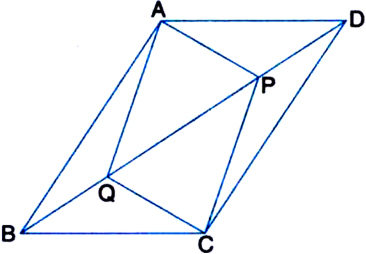
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see figure). AC is a diagonal. Show that:
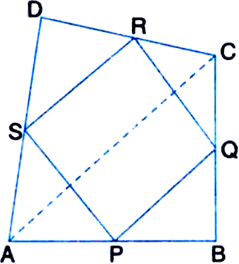
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Solution
Given: ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal.
To Prove:
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Proof : (i) In
S is the mid-pouint of DA and R is the mid-point of DC
SR 
AC and SR= 
AC
| MId-point therorem
(ii) In
P is the mid-pouint of AB and Q is the mid-point of BC
| Mid-point theorem
But from (i)
PQ = SR
To Prove:
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Proof : (i) In
S is the mid-pouint of DA and R is the mid-point of DC SR AC and SR= AC| MId-point therorem
(ii) In
P is the mid-pouint of AB and Q is the mid-point of BC| Mid-point theorem
But from (i)
PQ = SR
(iii) PQ || AC | From (ii)
SR || AC | From (i)
∴ PQ || SR
| Two lines parallel to the same line are parallel to each other
Also, PQ = SR | From (ii)
∴ PQRS is a parallelogram.
| A quadrilateral is a parallelogram if a pair of opposite sides are parallel and are of equal length
