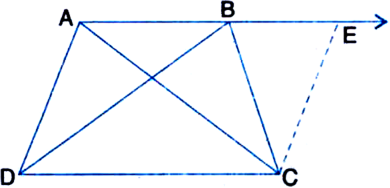
ABC is an isosceles triangle in which AB = AC. AD bisects ∠PAC and CD || AB. Show that
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram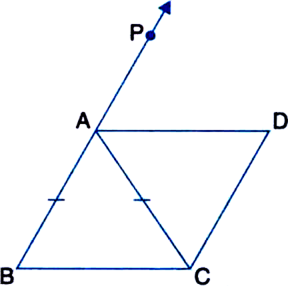
Given: ABC is an isosceles triangle in which AB = AC. AD bisects ∠PAC and CD || AB.
To Prove:
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram.
Proof:
(i) In ∆ABC,
∵ AB = AC
∴ ∠B = ∠C ...(1)
| Angles opposite to equal sides of a triangle are equal
Also, Ext. ∠PAC = ∠B + ∠C
| An exterior angle of a triangle is equal to the sum of two interior opposite angles
⇒ ∠PAC = ∠C + ∠C | From (1)
⇒ 2 ∠CAD = 2 ∠C | ∵ AD bisects ∠PAC
⇒ ∠CAD = ∠C
⇒ ∠DAC = ∠BCA
(ii) But these angles form a pair of equal alternate interior angles
∴ AD || BC
Also, CD || AB
∴ ABCD is a parallelogram
| A quadrilateral is a parallelogram if its both the pairs of opposite sides are parallel.