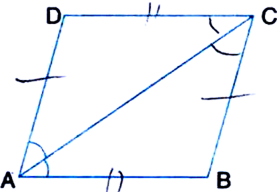
If a diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle and then the two diagonals are perpendicular to each other.

Solution

Given: ABCD is a ||gm. Diagonal AC bisects ∠A.
To Prove: (i) AC bisects ∠C
(ii) AC ⊥ BD.
Proof: (i) ∵ AB || DC and AC intersects them
∴ ∠1 = ∠4
| Alternate Interior ∠s
Similarly, ∠2 = ∠3
| Alternate Interior ∠s
But ∠1 = ∠2
∴ ∠3 = ∠4
⇒ AC bisects ∠C.
(ii) In ∆ADC,
∠2 = ∠4
∴ AD = CD
| Sides opposite to equal angles of a triangle are equal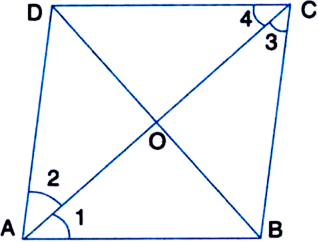

In ∆AOD and ∆COD,
OA = OC    | ∵ Diagonals
of a ||gm bisect each other
OD = OD    | Common side
AD = CD    | Proved above
∴ ∆AOD ≅ ∆COD
| SSS Congruence Axiom
∴ ∠AOD = ∠COD    | C.P.C.T.
But ∠AOD + ∠COD = 180°
| Linear Pair Axiom
⇒ 2∠AOD = 180°
| ∵ ∠AOD = ∠COD
⇒ ∠AOD = 90°
⇒    AC ⊥ BD.

Some More Questions From Circles Chapter

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:

(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.

In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram

(v) AC = DF
(vi) ∆ABC ≅ ∆DEF. [CBSE 2012

For Daily Free Study Material Join wiredfaculty

Circles

If a diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle and then the two diagonals are perpendicular to each other.

Some More Questions From Circles Chapter

If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Show that the diagonals of a square are equal and bisect each other at right angles.

Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i) it bisects ∠C also
(ii) ABCD is a rhombus.

ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:

(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

Circles

If a diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle and then the two diagonals are perpendicular to each other.

Some More Questions From Circles Chapter

If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Show that the diagonals of a square are equal and bisect each other at right angles.

Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:(i) it bisects ∠C also(ii) ABCD is a rhombus.

ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that: (i) ∆APD ≅ ∆CQB(ii) AP = CQ(iii) ∆AQB ≅ ∆CPD(iv) AQ = CP(v) APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:(i) ∆APB ≅ ∆CQD(ii) AP = CQ.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i) it bisects ∠C also
(ii) ABCD is a rhombus.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:

(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.