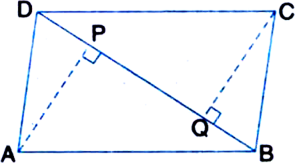
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see figure). Show that F is the midpoint of BC.
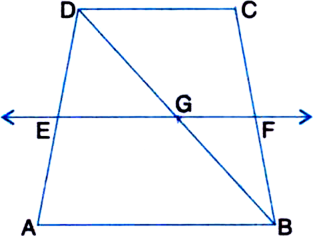
Given: ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F.
To Prove: F is the mid-point of BC.
Proof: Let DB intersect EF at G.
In ∆DAB,
∵ E is the mid-point of DA and EG || AB
∴ G is the mid-point of D
| By converse of mid-point theorem
Again, in ∆BDC,
∵ G is the mid-point of BD and GF || AB || DC
∴ F is the mid-point of BC.
| By converse of mid-point theorem