ABCD is a parallelogram and line segments AX, CY bisect the angles A and C respectively. Show that AX || CY.

Solution

Given: ABCD is a parallelogram and line segments AX, CY bisect the angles A and C respectively.
To Prove: AX || CY.
Proof: ∵ ABCD is a parallelogram.
∴ ∠A = ∠C    | Opposite ∠s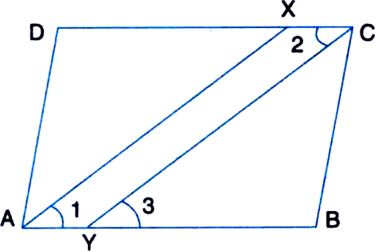

$rightwards double arrow space space space space 1 half angle straight A equals 1 half angle straight C$
| ∵ Halves of equals are equal
⇒ ∠1 = ∠2    ....(1)
| ∵ AX is the bisector of ∠A and CY is the bisector of ∠C
Now, AB || DC and CY intersects them
∴ ∠2 = ∠3    ...(2)
| Alternate interior ∠s
From (1) and (2), we get
∠1 = ∠3
But these form a pair of equal corresponding angles
∴ AX || CY.

Some More Questions From Circles Chapter

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:

(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.

For Daily Free Study Material Join wiredfaculty

Circles

ABCD is a parallelogram and line segments AX, CY bisect the angles A and C respectively. Show that AX || CY.

Some More Questions From Circles Chapter

If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Show that the diagonals of a square are equal and bisect each other at right angles.

Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i) it bisects ∠C also
(ii) ABCD is a rhombus.

ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:

(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

Circles

ABCD is a parallelogram and line segments AX, CY bisect the angles A and C respectively. Show that AX || CY.

Some More Questions From Circles Chapter

If the diagonals of a parallelogram are equal, then show that it is a rectangle.

Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Show that the diagonals of a square are equal and bisect each other at right angles.

Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:(i) it bisects ∠C also(ii) ABCD is a rhombus.

ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that: (i) ∆APD ≅ ∆CQB(ii) AP = CQ(iii) ∆AQB ≅ ∆CPD(iv) AQ = CP(v) APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:(i) ∆APB ≅ ∆CQD(ii) AP = CQ.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i) it bisects ∠C also
(ii) ABCD is a rhombus.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:

(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.