+91-8076753736[email protected]
logo
logo
-->

Circles

Question
CBSEENMA9002772
Wired Faculty App

In ∆ABC, AD is the median through A and E is the mid-point of AD. BE is produced to meet AC in F. Prove that 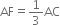 AF equals 1 third AC

Solution
Given: In ∆ABC, AD is the median through A and E is the mid-point of AD. BE is produced to meet AC in F.
To Prove: AF=1 third AC
Construction: Draw DG || EF to intersect AC in G.

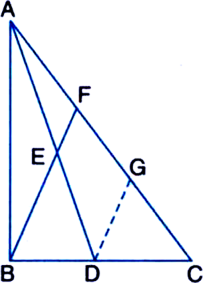
Proof: ∵ EF || DG    | by construction
and    AE = ED
| ∵ E is the mid-point of AD
∴ AF = FG    ...(1)
| A line drawn through the mid-point of a side of a triangle parallel to another side bisects the third side
Again,
DG || EF    | by construction
and    CD = DB
| ∵ D is the mid-point of
∴ BC FG = GC    ...(2)
| A line drawn through the mid-point of a side of a triangle parallel to another side bisects the third side
From (1) and (2),
AF = FG = GC
Now, AF + FG + GC = AC
⇒ AF + AF + AF = AC
| From (1) and (2)
⇒ 3 AF = AC

rightwards double arrow space space AF equals 1 third AC

Some More Questions From Circles Chapter

Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

 Show that the diagonals of a square are equal and bisect each other at right angles.

Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i)    it bisects ∠C also
(ii)    ABCD is a rhombus.

ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:

(i)    ∆APD ≅ ∆CQB
(ii)   AP = CQ
(iii)  ∆AQB ≅ ∆CPD
(iv)  AQ = CP
(v)   APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.

In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i)     quadrilateral ABED is a parallelogram
(ii)    quadrilateral BEFC is a parallelogram
(iii)   AD || CF and AD = CF
(iv)   quadrilateral ACFD is a parallelogram



(v)     AC = DF
(vi)    ∆ABC ≅ ∆DEF. [CBSE 2012

ABCD is a trapezium in which AB || CD and AD = BC (see figure): Show that
(i)      ∠A = ∠B
(ii)    ∠C = ∠D
(iii)    ∆ABC = ∆BAD
(iv)    diagonal AC = diagonal BD.



[Hint. Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation