C.
2Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i) it bisects ∠C also
(ii) ABCD is a rhombus.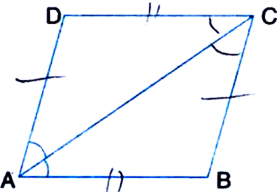
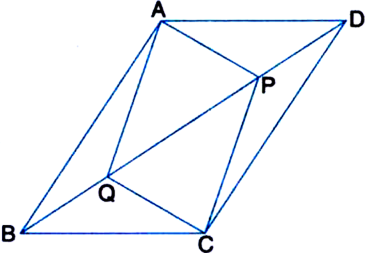
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.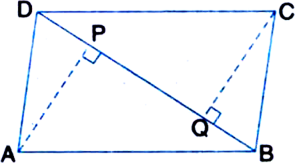
In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram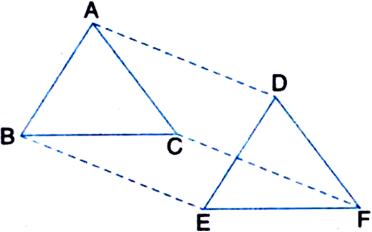
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF. [CBSE 2012
Mock Test Series
