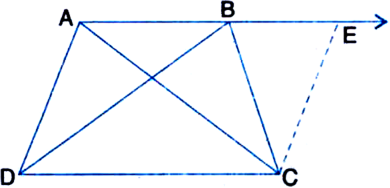
In the figure ABCD is a parallelogram and E is the mid-point of side BC. DE and AB on producing meet at F. Prove that AF = 2AB.
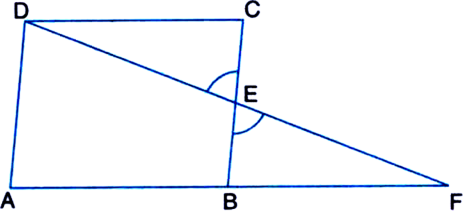
Given: ABCD is a parallelogram and E is the mid-point of side BC. DE and AB on producing meet at F.
To Prove: AF = 2AB
Proof: In ∆FAD,
∵ E is the mid-point of BC | Given
and EB || DA
| Opposite sides of a parallelogram are parallel
∴ B is the mid-point of AF | by converse of
mid-point theorem![]()