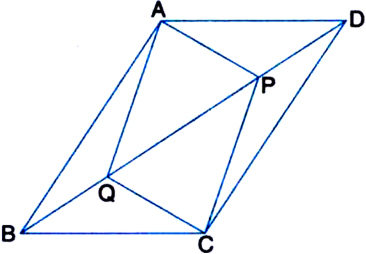
ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that 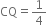 AC (see figure). If PQ produced meets BC at R, prove that R is the mid-point of BC.
AC (see figure). If PQ produced meets BC at R, prove that R is the mid-point of BC.
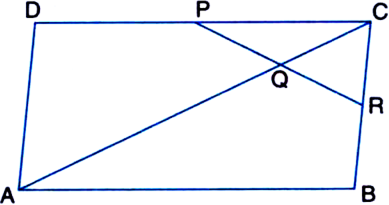
Given: ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that
AC. PQ produced meets BC at R.
To Prove: R is the mid-point of BC.
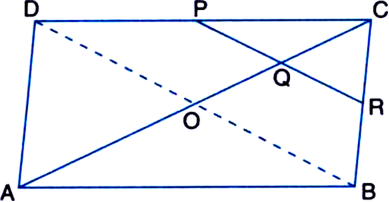
Construction: Join BD to intersect AC at O.
Proof: ∵ ABCD is a parallelogram and the diagonals of a parallelogram bisect each that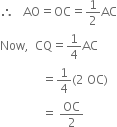
![]() Q is the mid-point of CO
Q is the mid-point of CO
In ∆CDO,
∵ P is the mid-point of DC and Q is the midpoint of CO
∴ PQ || DO | by mid-point theorem
⇒ PR || DB
⇒ QR || OB
Now, in ∆COB,
∵ Q is the mid-point of CO and QR || OB
∴ R is the mid-point of BC
| by converse of mid-point theorem