+91-8076753736[email protected]
logo
logo
-->

Circles

Question
CBSEENMA9002769
Wired Faculty App

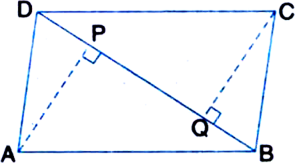
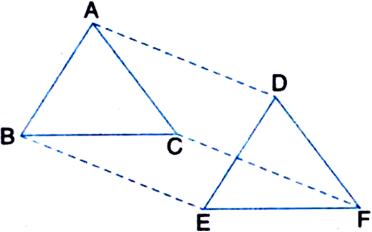
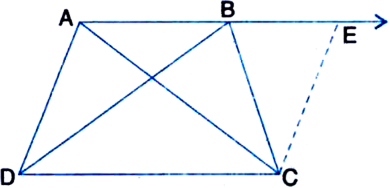
In triangle ABC, points M and N on sides AB and AC respectively are taken so that

AM equals 1 fourth AB space and space AN equals 1 fourth AC comma space Prove that MN = 1 fourth

Solution
Given: In triangle ABC, points M and N on the sides AB and AC respectively are taken so that
AM equals 1 fourth AB thin space and space AN equals 1 fourth AC
To Prove: MN equals 1 fourth BC.

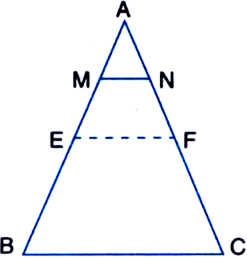
Construction: Join EF where E and F are the middle points of AB and AC respectively.
Proof: Y E is the mid-point of AB and F is the mid-point of AC.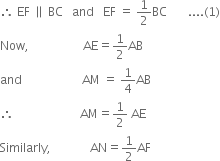
therefore space EF space parallel to space BC space space space and space space space EF space equals space 1 half BC space space space space space space space.... left parenthesis 1 right parenthesis Now comma space space space space space space space space space space space space space space space space space space AE equals 1 half AB and space space space space space space space space space space space space space space space space space space space space AM space equals space 1 fourth AB therefore space space space space space space space space space space space space space space space space space space space space space space AM equals 1 half space AE Similarly comma space space space space space space space space space space space space space AN equals 1 half AF
rightwards double arrow  M and N are the mid-points of AE and AF respectively.
therefore space MN space parallel to space EF space and space MN space equals space 1 half space EF equals 1 half open parentheses 1 half BC close parentheses
                                                           | From (1)
                                 equals 1 fourth BC.

Some More Questions From Circles Chapter

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.

In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i)     quadrilateral ABED is a parallelogram
(ii)    quadrilateral BEFC is a parallelogram
(iii)   AD || CF and AD = CF
(iv)   quadrilateral ACFD is a parallelogram



(v)     AC = DF
(vi)    ∆ABC ≅ ∆DEF. [CBSE 2012

ABCD is a trapezium in which AB || CD and AD = BC (see figure): Show that
(i)      ∠A = ∠B
(ii)    ∠C = ∠D
(iii)    ∆ABC = ∆BAD
(iv)    diagonal AC = diagonal BD.



[Hint. Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]

In a parallelogram, show that the angle bisectors of two adjacent angles intersect at right angles.

If a diagonal of a parallelogram bisects one of the angles of the parallelogram, it also bisects the second angle and then the two diagonals are perpendicular to each other.

 “A diagonal of a parallelogram divides it into two congruent triangles.” Prove it.

Show that the diagonals of a square are equal and perpendicular to each other.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation