+91-8076753736[email protected]
logo
logo
-->

Circles

Question
CBSEENMA9002764
Wired Faculty App

ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

Solution
Given: ABCD is a rectangle. P, Q, R and S are the mid-points of AB, BC, CD and DA respectively. PQ, QR, RS and SP are joined.

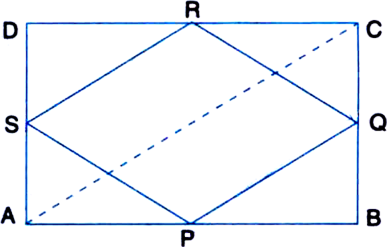
To Prove: Quadrilateral PQRS is a rhombus.
Construction: Join AC.
Proof: In ∆ABC,
because space space space P and Q are the mid-points of AB and BC respectively.
therefore space space space PQ space parallel to space AC space and space PQ equals 1 half AC space space space space space space space space space... left parenthesis 1 right parenthesis
In increment ADC comma
because S and R are the mid-points of AD and DC respectively.
therefore space space space SR space parallel to space AC space and space SR space equals space 1 half space AC space space space space space space space.... left parenthesis 2 right parenthesis
From (1) and (2),
PQ space parallel to space SR space and space PQ space equals space SR
therefore   Quardrilateral PQRS is a parallelogram      ....(3_
In rectangle ABCD,
   AD = BC                    | Opposite sides
rightwards double arrow space space space 1 half AD equals 1 half BC
                  | Halves of equals are equal
rightwards double arrow      AS = BQ
In increment APS space and space increment BPQ
AP = BP
| ∵ P is the mid-point of AB
AS = BQ    | Proved above
∠PAS = ∠PBQ    | Each = 90°
∴ ∆APS ≅ ∆BPQ
| SAS Congruence Axiom
∴ PS = PQ    ...(4) | C.P.C.T.
In view of (3) and (4), PQRS is a rhombus.

Some More Questions From Circles Chapter

Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i)    it bisects ∠C also
(ii)    ABCD is a rhombus.

ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:

(i)    ∆APD ≅ ∆CQB
(ii)   AP = CQ
(iii)  ∆AQB ≅ ∆CPD
(iv)  AQ = CP
(v)   APCQ is a parallelogram.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.

In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i)     quadrilateral ABED is a parallelogram
(ii)    quadrilateral BEFC is a parallelogram
(iii)   AD || CF and AD = CF
(iv)   quadrilateral ACFD is a parallelogram



(v)     AC = DF
(vi)    ∆ABC ≅ ∆DEF. [CBSE 2012

ABCD is a trapezium in which AB || CD and AD = BC (see figure): Show that
(i)      ∠A = ∠B
(ii)    ∠C = ∠D
(iii)    ∆ABC = ∆BAD
(iv)    diagonal AC = diagonal BD.



[Hint. Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]

In a parallelogram, show that the angle bisectors of two adjacent angles intersect at right angles.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation