गणित Chapter 11 रचनाएँ
Sponsor Area
NCERT Solution For Class 10 गणित गणित
7.6 cm लंबा एक रेखाखंड खींचिए और इसे 5:8 अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।
रचना के चरण:
(i) पैमाने की सहायता से 7.6cm लंबा एक रेखाखंड AB खींचिए।
(ii) AB से एक न्यून कोण बनाती हुई किरण AX खींचिए।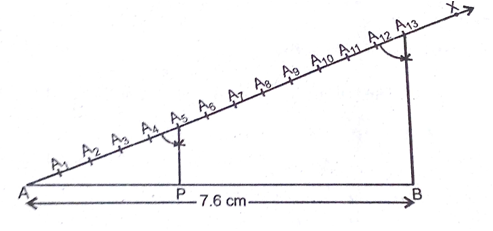
(iii) किरण AX पर 13(5+8) बिंदु A1, A2, A3, A4, A5, A6, A7, A8, A9, A10, A11, A12 और A13 इस प्रकार अंकित कीजिए कि AA1 = A1A2 = A2A3 = A3A4= A4A5 = A5A6 = A6A7 = A7A8 = A8A9 = A9A10 = A10A11 = A11A12=A12A13 हो।
(iv) A13B को मिलाइए।
(v) A5 से A5P || A13B खींचने के लिए बिंदु A5 पर  बनाइए।
बनाइए।
(vi) इस प्रकार प्राप्त बिंदु P अभीष्ट बिंदु है जो AB को 5:8 के अनुपात में विभाजित करता है।
(vii) पैमाने के सहायता से दोनों भागों को मापने पर AP = 2.9 cm तथा PB = 4.7cm (लगभग) प्राप्त होते हैं।
प्रतिपादन - त्रिभुज ABA13 में A5P || A13B है।
अत: आधारभूत समानुपातिका प्रमेय से,
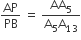
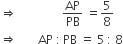
4cm, 5cm और 6cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 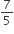 गुनी हों।
गुनी हों।
(i) पैमाने की सहायता से 6cm लम्बा एक रेखाखण्ड BC खींचिए।
(ii) B को केंद्र तथा त्रिज्या 5cm लेकर एक चाप BC के ऊपर की ओर लगाइए।
(iii) C को केंद्र तथा त्रिज्या 4cm लेकर एक चाप BC के ऊपर की ओर लगाइए जो चरण (ii) की चाप को A पर प्रतिच्छेद करें।
(iv) AB तथा AC को मिलाकर अभीष्ट
 प्राप्त कीजिए।
प्राप्त कीजिए।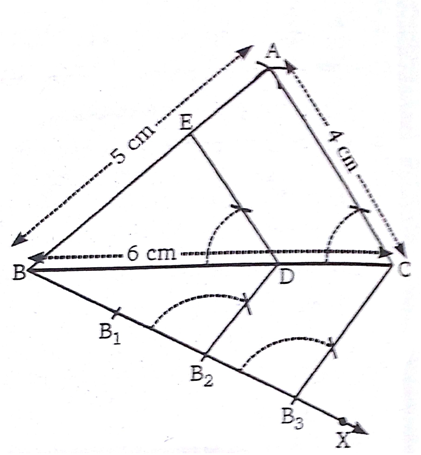
(v) अब BC के नीचे की ओर एक न्यून कोण CBX बनाइए।
(vi) किरण BX पर तीन बिंदु B1B2 तथा B3 इस प्रकार अंकित कीजिए कि
BB1 = B1B2 = B2B3 हो।
(vii) B3C को मिलाइए।
(viii) B2 से B2D || B3C खींचने के लिए बिंदु B2 पर
 बनाइए तथा B2D को मिलाइए।
बनाइए तथा B2D को मिलाइए।(ix) अब बिंदु D से DE || AC खींचने के लिए
 बनाइए जो AB को E पर काटे।
बनाइए जो AB को E पर काटे।इस प्रकार EBD वांछित त्रिभुज है जिसकी भुजाएँ दी गई
 की भुजाओं की
की भुजाओं की  गुनी है।
गुनी है।प्रतिपादन:
 में
में  है।
है।
 (AAA समरूपता से)
(AAA समरूपता से)
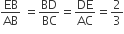
5cm, 6cm और 7cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ, दिए हुए त्रिभुज की संगत भुजाओं की 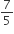 गुनी हों।
गुनी हों।
(i) एक त्रिभुज ABC बनाइए जिसकी भुजाएँ AB = 7cm, BC = 6cm तथा AC = 5cm हों।
(ii) बिंदु A से एक किरण AX, रेखाखण्ड AB के साथ न्यून कोण बनाते हुए खींचिए।
(iii) किसी चाप की परकार खोलकर रेखा AX को सात बराबर AX1, X1X2, X2X3, X3X4, X4X5, X5X6, X6X7 भागों में बाँटिए।
(iv) X5 को B से मिलाइए।
(v) X7 से X7B'|| X5B खींचिए जो AB को बढ़ाने पर B' पर मिले।
(vi) B' से B'C'||BC खींचिए जो AC को बढ़ाने पर C' मिले।
(vii) इस प्रकार
 अभीष्ट त्रिभुज है जिसकी भुजाएँ
अभीष्ट त्रिभुज है जिसकी भुजाएँ  की भुजाओं का
की भुजाओं का 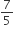 वां भाग हैं।
वां भाग हैं।प्रतिपादन:
 में BC || B'C' है।
में BC || B'C' है।
 (AAA समरूपता से)
(AAA समरूपता से)
आधार 8cm तथा ऊँचाई 4cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ पर समद्विबाहु त्रिभुज की संगत भुजाओं की 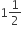 गुनी हों।
गुनी हों।
(i) पैमाने की सहायता से 8 cm लंबा एक रेखाखण्ड BC खींचिए।
(ii) BC रेखाखण्ड का लंब समद्विभाजक PQ खींचिए जो BC को M पर मिले।
(iii) M को केंद्र मानकर 4cm त्रिज्या की परकार से AM = 4cm काटिए।
(iv) AB तथा AC को मिलाकर अभीष्ट
 प्राप्त कीजिए।
प्राप्त कीजिए।(v) अब BC को D तक इस प्रकार बढ़ाइए कि BD = 12 cm प्राप्त हो क्योंकि
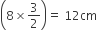
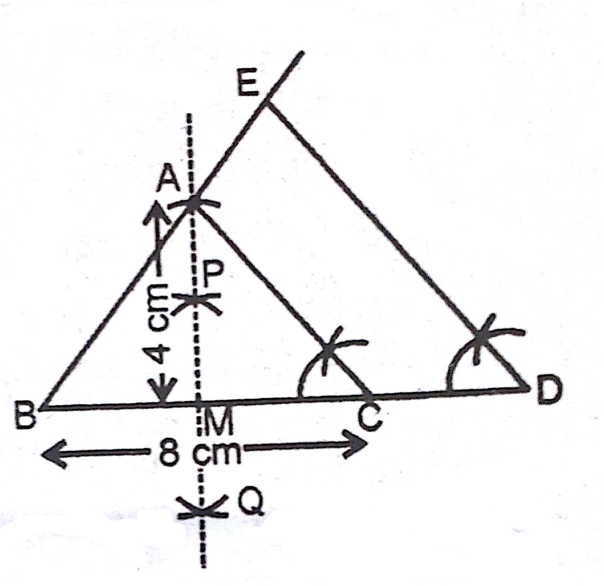
होता है।
(vi) D से DE||AC खींचने के लिए
 बनाइए जो BA को बढ़ाने पर E पर मिले।
बनाइए जो BA को बढ़ाने पर E पर मिले। (vii) इस प्रकार EBD अभीष्ट त्रिभुज है जिसकी संगत भुजाएँ समद्विबाहु त्रिभुज ABC की भुजाओं का
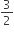 गुना है।
गुना है। प्रतिपादन:
 में AC||DE है।
में AC||DE है। 
 (AAA समरूपता से)
(AAA समरूपता से)
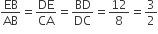
एक त्रिभुज ABC बनाइए, जिसमें BC = 6cm, AB = 5cm और  हो। फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ
हो। फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ  की संगत भुजाओं की
की संगत भुजाओं की 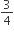 गुनी हों।
गुनी हों।
रचना के चरण:
(1) पैमानों की सहायता से 6cm लंबा एक रेखाखंड BC खींचिए।
(2) बिंदु B पर परकार की सहायता से  बनाइए।
बनाइए।
(3) B को केंद्र मानकर 5 cm की त्रिज्या वाली परकार द्वारा BA= 5cm काटिए।
(4) AC को मिलाकर  प्राप्त कीजिए।
प्राप्त कीजिए।
(5) अब BC के नीचे की ओर एक न्यून कोण CBY बनाइए।
(6) किरण BY पर चार बिंदु B1, B2, B3, व B4 इस प्रकार अंकित करें कि BB1 = B1B2 = B2B3 = B3B4 हों।
(7) B4C को मिलाइए।
(8) B3 से B3D || B4C खींचने के लिए  बनाइए जो BC को D पर काटे।
बनाइए जो BC को D पर काटे।
(9) अब D से DE || AC खींचने के लिए  बनाइए जो AB को E पर मिले।
बनाइए जो AB को E पर मिले।
इस प्रकार EBD वांछित त्रिभुज है जिसकी भुजाएँ दी गई जो  की भुजाओं की
की भुजाओं की 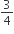 गुनी हैं।
गुनी हैं।
प्रतिपादन:  में DE || AC
में DE || AC
 (AAA समरूपता से)
(AAA समरूपता से)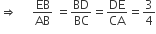
एक त्रिभुज ABC बनाइए, जिसमें BC = 7cm, 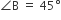 ,
,  हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ
हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ  की संगत भुजाओं की
की संगत भुजाओं की  गुनी हों।
गुनी हों।
(i) पैमाने की सहायता से 7cm लंबा एक रेखाखंड BC खींचिए।
(ii) परकार की सहायता से
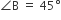 व
व 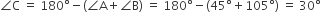 की रचना कीजिए। जो परस्पर बिंदु A पर मिले।
की रचना कीजिए। जो परस्पर बिंदु A पर मिले।(iii) BC के नीचे की ओर एक न्यून कोण बनाती हुई किरण BX खींचिए।

(iv) किरण BX पर चार बिंदु B1, B2, B3 व B4 इस प्रकार अंकित करें कि BB1 = B1B2 = B2B3 = B3B4 हों।
(v) B3C को मिलाइए।
(vi) बिंदु B4C से B4D || B3C खींचने के लिए खींचिए
 खींचिए जो BC को बढ़ाने पर D पर मिले।
खींचिए जो BC को बढ़ाने पर D पर मिले।(vii) अब बिंदु D से DE||AC खींचने के लिए
 बनाइए जो BA को बढ़ाने पर पर E पर मिले।
बनाइए जो BA को बढ़ाने पर पर E पर मिले। इस प्रकार अभीष्ट त्रिभुज है जिसकी भुजाएँ त्रिभुज ABC की भुजाओं की
 गुनी हैं।
गुनी हैं।प्रतिपादन -
 में AC || DE
में AC || DE
 (AAA समरूपता से)
(AAA समरूपता से) 
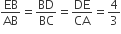
एक समकोण त्रिभुज की रचन कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4cm तथा 3cm लंबाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की  गुनी हों।
गुनी हों।
(i) पैमाने की सहायता से 4 cm लम्बा एक रेखाखण्ड BC खींचिए।
(ii) बिंदु B पर परकार की सहायता से
 का कोण बनाइए।
का कोण बनाइए।(iii) B को केंद्र तथा 3 cm त्रिज्या के परकार खोलकर, BA = 3 cm काटिए।
(iv) AC को मिलाइए जिसमें अभीष्ट त्रिभुज ABC प्राप्त हो।
(v) BC के नीचे की ओर एक न्यून कोण बनती हुई किरण BX खींचिए।

(vi) किरण BX पर पाँच बिंदु B1, B2, B3, B4 तथा B5 इस प्रकार अंकित करें कि BB1 = B1B2 = B2B3 = B3B4 = B4B5 हों।
(vii) B3C को मिलाइए तथा B5 से B5D || B3C खींचने के लिए
 बनाइए जो BC को बढ़ाने पर D पर मिले।
बनाइए जो BC को बढ़ाने पर D पर मिले।(viii) अब बिंदु D से DE || CA खींचने के लिए
 बनाइए जो BA को बढ़ाने पर E पर काटे।
बनाइए जो BA को बढ़ाने पर E पर काटे।इसी प्रकार EBD अभीष्ट त्रिभुज है जिसकी भुजाएँ
 की भुजाओं की
की भुजाओं की  गुनी हों।
गुनी हों। प्रतिपादन:
 में DE || CA
में DE || CA∴
 (AAA समरूपता से)
(AAA समरूपता से)
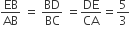
6cm त्रिज्या का एक वृत्त खींचिए। केंद्र से दूर स्थित एक बिंदु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए और उनकी लंबाइयाँ मापिए।
(1) O को केंद्र मानकर त्रिज्या की चाप द्वारा एक वृत्त खींचिए।
(2) O से 10 cm की दूरी पर एक बिंदु P लीजिए।

(3) O व P को मिलाइए।
(4) OP को बिंदु M पर समद्विभाजित कीजिए।
(5) अब M को केंद्र मानकर तथा OM को त्रिज्या लेकर एक वृत्त खींचिए जो दिए हुए वृत्त को Q तथा R पर प्रतिच्छेदित करे।
(6) PQ तथा PR को मिलाइए। यही PQ तथा PR वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।
(7) मापने पर PQ = PR = 8 cm है।
4 cm त्रिज्या के एक वृत्त पर 6cm त्रिज्या के एक सकेंद्रीय वृत्त के किसी बिंदु से एक स्पर्श रेखा की रचना कीजिए और उसकी लंबाई मापिए। परिकलन से इस माप की जाँच भी कीजिए।
(i) O को केंद्र मानकर 4cm त्रिज्या तथा 6cm त्रिज्या की चाप द्वारा दो सकेंद्रीय वृत्त खींचिए।
(ii) बड़े वृत्त की परिधि पर एक बिंदु P अंकित करें।
(iii) OP को मिलाकर इसका लंब समद्विभाजिक M प्राप्त कीजिए।
(iv) अब M को केंद्र मानकर तथा OM को त्रिज्या लेकर एक वृत्त खींचिए जो छोटे वृत्त को Q तथा R पर प्रतिच्छेद करे।
(v) PQ तथा PR को मिलाइए। यही PQ तथा PR छोटे वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।
(vi) मापने पर PQ = PR = 4.5 cm (लगभग) हैं।

जाँच - OQ को मिलाकर समकोण प्राप्त कीजिए।
अब समकोण
 में,
में,OQ = 4cm, OP = 6cm

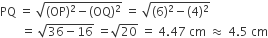
3cm त्रिज्या का एक वृत्त खींचिए। इसके किसी बढ़ाए गए व्यास पर केंद्र से 7cm की दूरी पर स्थित दो बिंदु P और Q लीजिए। इन दोनों बिंदुओं से वृत्त पर स्पर्श रेखाएँ खींचिए।
(i) O को केंद्र मानकर 3cm त्रिज्या की चाप द्वारा एक वृत्त खींचिए।
(ii) वृत्त के एक व्यास AOB को P और Q तक इस प्रकार बढ़ाए कि OP = OQ = 7 cm हो।
(iii) OP तथा OQ के लंब समद्विभाजिक क्रमश: तथा प्राप्त कीजिए।
(iv) अब M1 को केंद्र तथा M1P को त्रिज्या मानकर एक वृत्त खींचिए जो दिए गए वृत्त को T1 व T2 पर प्रतिच्छेद करे।
(v) PT1 तथा PT2 को मिलाइए। इस प्रकार PT1 तथा PT2 बिंदु P से स्पर्श रेखाएँ हैं।
(vi) इसी प्रकार M2 को केंद्र तथा M2Q को त्रिज्या मानकर एक वृत्त खींचिए जो दिए गए वृत्त को T3 व T4 पर प्रतिच्छेद करे।
(vii) QT3 तथा QT4 को मिलाइए। इस प्रकार QT3 तथा QT4 बिंदु Q से स्पर्श रेखाएँ हैं।
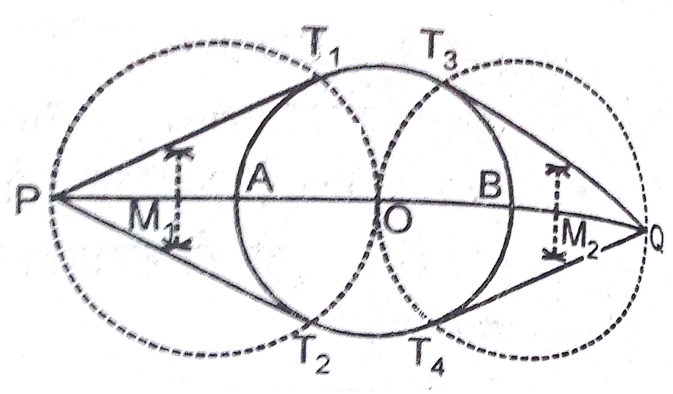
5cm त्रिज्या के एक वृत्त पर ऐसी दो स्पर्श रेखाएँ खींचिए, जो परस्पर  के कोण पर झुकी हों।
के कोण पर झुकी हों।
(i) O को केंद्र मानकर 5cm त्रिज्या लेकर एक वृत्त खींचिए।
(ii) वृत्त के किसी त्रिज्या OR से
 का कोण लेकर एक त्रिज्या OQ खींचिए।
का कोण लेकर एक त्रिज्या OQ खींचिए।
(iii) वृत्त की त्रिज्याओं OR तथा OQ के बिंदु R तथा Q पर
 का कोण बनाइए।
का कोण बनाइए।(iv) इस प्रकार PR तथा PQ वृत्त की अभीष्ट स्पर्श रेखाएँ हैं जो
 के कोण पर झुकी हैं।
के कोण पर झुकी हैं।8cm लंबा एक रेखाखंड AB खींचिए। A को केंद्र मानकर 4cm त्रिज्या का एक वृत्त तथा B को केंद्र लेकर 3 cm त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रेखाओं की रचना कीजिए।
(1) पैमाने की सहायता से AB = 8cm लंबा एक रेखाखंड खींचिए।
(2) A को केंद्र मानकर 4cm त्रिज्या की परकार द्वारा एक वृत्त खींचिए जो AB को O पर मिले।
(3) इसी प्रकार B को केंद्र मानकर 3cm त्रिज्या की परकार द्वारा एक वृत्त खींचिए।
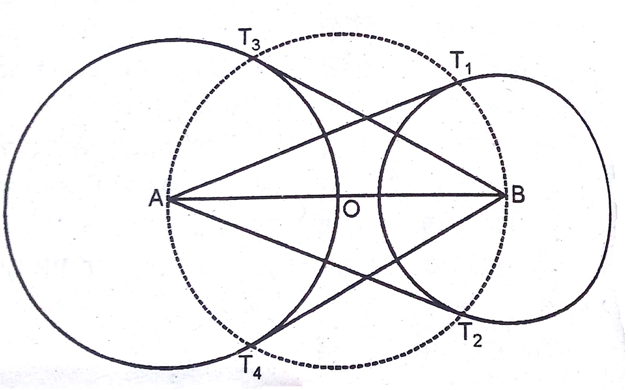
(4) स्पष्ट बिंदु O रेखाखंड AB का मध्य-बिंदु है। अब O को केंद्र तथा OA या OB को त्रिज्या मानकर एक वृत्त खींचिए जो केंद्र B वाले वृत्त को T1 व T2 तथा केंद्र A वाले वृत्त को T3 व T4 पर प्रतिच्छेद करता है।
(5) AT1, AT2, BT3 तथा BT4 को मिलाने पर वांछित स्पर्श रेखाएँ प्राप्त हो जाती हैं।
माना ABC एक समकोण त्रिभुज है, जिसमें AB = 6cm, BC = 8cm तथा  हैं। B से AC पर BD लंब हैं। बिंदुओं B, C, D से होकर जाने वाला एक वृत्त खींचा गया हैं। A से इस वृत्त पर स्पर्श रेखा की रचना कीजिए।
हैं। B से AC पर BD लंब हैं। बिंदुओं B, C, D से होकर जाने वाला एक वृत्त खींचा गया हैं। A से इस वृत्त पर स्पर्श रेखा की रचना कीजिए।
(1) पैमाने की सहायता से लंबा एक रेखाखण्ड खींचिए।
(2) B पर
 का कोण बनाइए तथा BA = 6 cm काटिए।
का कोण बनाइए तथा BA = 6 cm काटिए।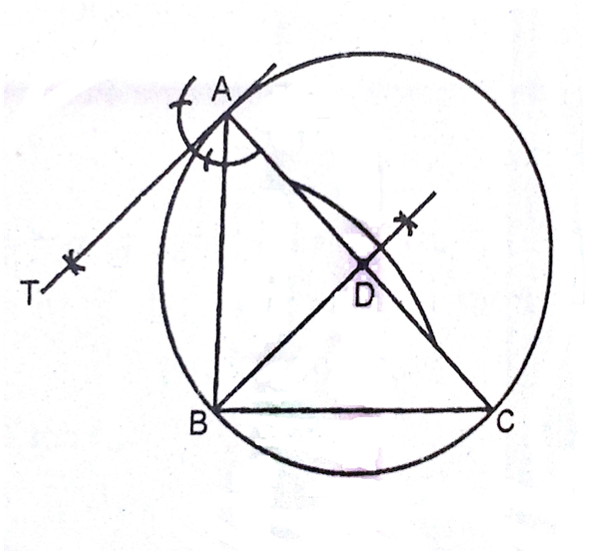
(3) A और C को मिलाकर समकोण
 प्राप्त कीजिए।
प्राप्त कीजिए।(4) बिंदु B से
 खींचिए जो AC को D पर काटे।
खींचिए जो AC को D पर काटे।(5) अब D को केंद्र तथा DA या DB या DC को त्रिज्या लेकर एक वृत्त खींचिए।
(6) A पर
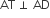 खींचिए जो वृत्त की स्पर्श रेखा होगी।
खींचिए जो वृत्त की स्पर्श रेखा होगी।
किसी चूड़ी की सहायता से एक वृत्त खींचिए। वृत्त के बाहर एक बिंदु लीजिए। इस बिंदु से वृत्त पर स्पर्श रेखाओं की रचना कीजिए।
(i) एक चूड़ी लेकर उसे अपनी कॉपी पर रखकर पैंसिल की सहायता से एक वृत्त खींचिए।
(ii) वृत्त के बाहर दिए बिंदु A से एक छेदक रेखा ARS खींचिए तथा इसे C तक इस प्रकार बढ़ाइए कि AR = AC हो।
(iii) अब CS को व्यास मानकर एक अर्धवृत्त की रचना कीजिए।
(iv) बिंदु A पर
 खींचिए जो अर्धवृत्त को B पर प्रतिच्छेद करे।
खींचिए जो अर्धवृत्त को B पर प्रतिच्छेद करे।(v) अब A को केंद्र तथा AB को त्रिज्या मानकर एक चाप लगाइए जो दिए गए वृत्त को T1 व T2 पर प्रतिच्छेद करे।
(vi) AT1 तथा AT2 को मिलाने पर वांछित स्पर्श रेखाएँ प्राप्त होती हैं।
एक मीनार के शिखर से एक 50 मी ऊँचे भवन के शिखर तथा पाद के अवनमन कोण क्रमशः 450 तथा 600 हैं। मीनार की ऊँचाई ज्ञात कीजिए। 
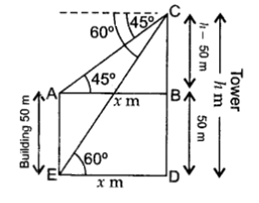
माना AE इमारत और CD मीनार है,
माना मीनार की ऊँचाई = h m
दिया है,
BD = AE = 50 m
एक 8 सेमी लम्बाई का रेखाखण्ड खींचिए तथा उसे 4:5 के अनुपात में आंतरिक रूप से विभाजित कीजिए।
1) एक रेखाखंड AB = 8 सेमी खींचा
2) AX के साथ कोण ∠BAX = 60 AB के साथ एक किरण बनाई।
3) AX के समानांतर करके किरण को एक कोण बनाकर ∠ABY = ∠BAX हैं।
4) AX पर चार अंक A1, A2, A3, A4 और पांच अंक B1, B2, B3, B4, B5 पर BY इस तरह से AA1 = A1A2 = A2A3 = A3A4।
5) A4B5 में शामिल हैं।
6) इस रेखा को एक बिंदु P पर AB को एक दूसरे को घुमाने दिया।
इस प्रकार, P, रेखा खंड AB आंतरिक रूप से 4: 5 के अनुपात में विभाजित होने वाला बिंदु है।
दी गई आकृति में, किसी बाह्य बिंदु P से वृत्त पर स्पर्श रेखाएँ PA तथा PB खींची गई हैं। CD एक अन्य स्पर्श रेखा है जो वृत्त को बिंदु Q पर स्पर्श करती है। यदि PA = 12 सेमी तथा QC = QD = 3 सेमी हो, तो PC + PD का मान ज्ञात कीजिए।
दिया है: PA और PB वृत्त की स्पर्शरेखा हैं।
PA = 12 सेमी
QC = QD = 3 सेमी
ज्ञात करने के लिए : PC + पद
PA = PB = 12 सेमी
(एक बाहरी बिंदु से एक सर्कल में खींची गई स्पर्शरेखा की लंबाई बराबर होती है)
इसी प्रकार, QC = AC = 3 सेमी
और QD = BD = 3 सेमी
अब, PC = PA − AC = 12 − 3 = 9 सेमी
इसी प्रकार, PD = PB − BD = 12 − 3 = 9 सेमी
अत:, PC + PD = 9 + 9 = 18 सेमी
Sponsor Area
एक त्रिभुज ABC बनाइए जिसमें BC = 6 सेमी, AB = 5 सेमी और ∠ABC = 60° हो । फिर एक त्रिभुज । की रचना कीजिए, जिसकी भुजाएँ △ABC की संगत भुजाओं की 3/4 गुनी हों।

(i) एक रेखा खंड बनाइये ,BC = 6 cm,एक रेखा BX बनाइये जो की 60 का कोण बना रहा हो BC के साथ
(ii) B से 5 सेमी की त्रिज्या का एक चाप खींचें ताकि यह A पर BX को काट सके।
(iii) अब △ABC बनाने के लिए AC को शामिल करें
(iv) रेखा खंड पर 4 बिंदु B1, B2, B3, B4 जो निम्न प्रकार से होंगे BB1 = B1B2 = B2B3 = B3B4
(vi) B4C को जोड़े और अब एक रेखा B3 से बनाए जो B4C के समानांतर हो जो BC को C' पर काट रही हो
(v) अब C' से एक रेखा बनाए जो AC के समानांतर हो और वो AB को A' पर काट रही हो
(vi) △A'BC' आवश्यक त्रिकोण है।
Mock Test Series
Sponsor Area
Sponsor Area





