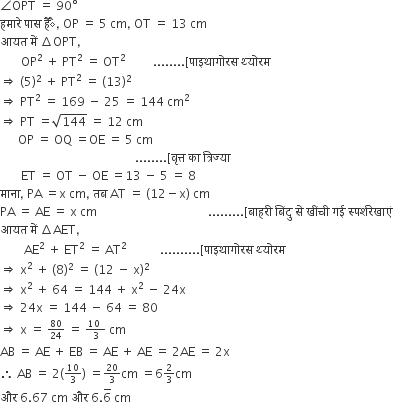गणित Chapter 10 वृत्त
Sponsor Area
NCERT Solution For Class 10 गणित गणित
एक वृत्त की कितनी स्पर्श रेखाएँ हो सकती हैं?
एक वृत्त की अपरिमित रूप से अनेक स्पर्श रेखाएँ हो सकती हैं।
5 सेमी त्रिज्या वाले एक वृत्त के बिंदु P पर स्पर्श रेखा PQ केंद्र O से जाने वाली एक रेखा से बिंदु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी। PQ की लंबाई है:
-
12 सेमी
-
13 सेमी
-
8.5 सेमी
-
 सेमी
सेमी
D.
 सेमी
सेमी

प्रश्नानुसार,
 [∵ स्पर्श बिंदु पर स्पर्श रेखा की त्रिज्या लम्बवत्त होती है]
[∵ स्पर्श बिंदु पर स्पर्श रेखा की त्रिज्या लम्बवत्त होती है]OP = 5cm
OQ = 12 cm
अब समकोण
 में,
में,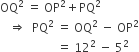
 PQ=
PQ= 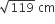
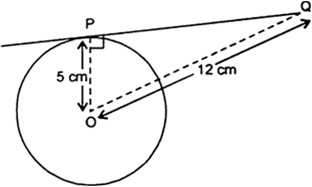
एक बिंदु Q से एक वृत्त पर स्पर्श रेखा की लंबाई 24cm तथा Q की केंद्र से दूरी 25 cm है। वृत्त की त्रिज्या है-
-
7cm
-
12cm
-
15 cm
-
24.5 cm
A.
7cm
दिए गए वृत्त का केंद्र लेने पर वृत्त की स्पर्श रेखा तथा वृत्त की त्रिज्या है परन्तु त्रिज्या और स्पर्श रेखा के बीच का कोण होता है।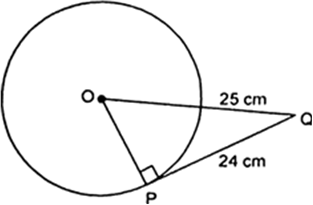
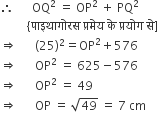
सलंग्न आकृति में, यदि TP, TO केंद्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि  तो
तो  बराबर है-
बराबर है-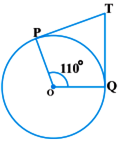
क्योंकि स्पर्श रेखा और त्रिज्या के बीच का कोण  होता है।
होता है।
 व
व 
 व
व 
चतुर्भुज POQT में,

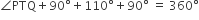



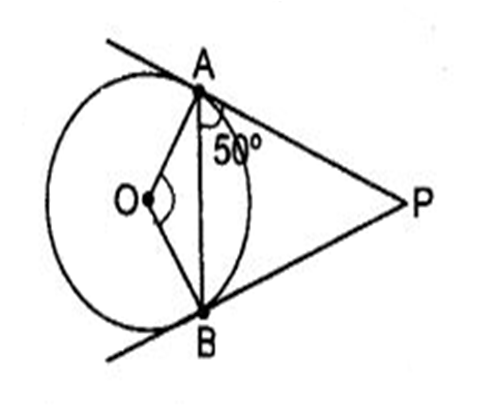
यदि एक बिंदु P से O केंद्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर  के कोण पर झुकी हों, तो
के कोण पर झुकी हों, तो  बराबर है:
बराबर है:
- 50°
- 60°
- 70°
- 80°
A.
50°ΔPOA और ΔPOB में,
PA = PB (बाह्य बिंदु से समान स्पर्श रेखाएँ)
OA = OB (वृत्त की त्रिज्याएँ)
और OP = OP (उभयनिष्ठ)
∴ ΔPOA ≅ ΔPOB (SSS सर्वांगसमता)
⇒ 
⇒ 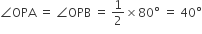
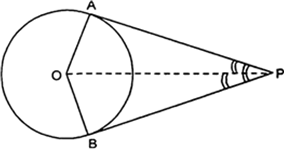
हम जानते हैं कि वृत्त की त्रिज्या और स्पर्श रेखा के बीच 90° का कोण होता है।
∴ 
अब ΔOAP में,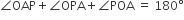
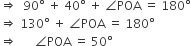
सिद्ध कीजिए की किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ होती हैं।
माना AB और CD स्पर्श रेखा वृत्त को P तथा Q पर स्पर्श करती हैं।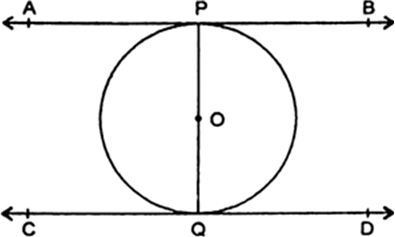
हम जानते हैं की स्पर्श बिंदु पर स्पर्श रेखा और त्रिज्या लम्बवत्त होते हैं।
∴  = 90° ....(i)
= 90° ....(i)
और  ...(ii)
...(ii)
समीकरण (i) तथा समीकरण (ii) के प्रयोग से, [∵ वैकल्पिक आंतरिक कोण]
[∵ वैकल्पिक आंतरिक कोण]
∴ AB || CD.
सिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त से होकर जाता है।
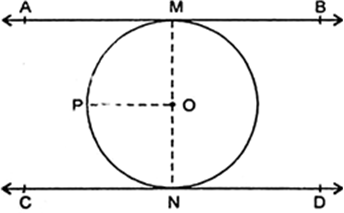
माना AMB तथा CND दो समांतर स्पर्श रेखाएँ है जो O केंद्र वाले वृत्त को M तथा N पर स्पर्श करती हैं। OP || AB खींचें।
अब, AM || PO
⇒ 
(क्रमागत आंतरिक कोण है)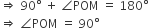
इसी प्रकार, 

अत: स्पर्श रेखा पर खींचा गया MON लंब वृत्त के केंद्र से होकर गुजरता है।
एक बिंदु A से, जो एक वृत्त के केंद्र से 5 cm दूरी पर है, वृत्त पर स्पर्श रेखा की लंबाई 4cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
हम जानते हैं कि स्पर्श बिंदु पर स्पर्श रेखा और त्रिज्या लम्बवत्त होते हैं।

दिया गया हैं OQ = 5 cm
PQ = 4 cm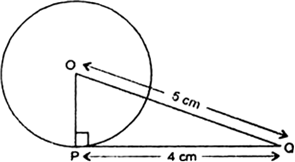
समकोण ΔOPQ में,
OQ2 = OP2 + PQ2
[पाइथागोरस प्रमेय के प्रयोग से]
OP2 = OQ2 – PQ2
⇒ OP2 = (5)2 – (4)2
= 25 – 16 = 9
⇒ OP = 3 cm
अत: वृत्त की त्रिज्या = 3 cm
दो सकेंद्रीय वृत्तों की त्रिज्याएँ 5cm तथा 3cm हैं। बड़े वृत्त की उस जीवा की लंबाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
माना, दिए गए दो सकेंद्रीय वृत्तों का केंद्र O है तथा PQ बड़े वृत्त की जीवा है जो छोटे वृत्त को बिंदु M पर स्पर्श करती है।
OP तथा OM को मिलाओ।
हम जानते हैं कि स्पर्श रेखा और त्रिज्या परस्पर लम्बवत्त होती है।
∴ 
अब, समकोण ΔOMP में,
OP2 = OM2 + PM2
[पाइथागोरस प्रमेय के प्रयोग से]
⇒ (5)2 = (3)2 + PM2
⇒ 25 = 9 + PM2
⇒ PM2 = 16
⇒ PM = 4 cm
PM = MQ = 4 cm
∴ PQ = 2 PM = 2 x 4 = 8 cm
अत: जीवा AB की लंबाई = 8 cm
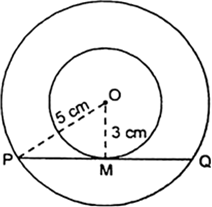
एक वृत्त के परिगत एक चतुर्भुज खींचा गया है (देखिए सलंग्न आकृति)। सिद्ध कीजिए:
AB + CD = AD + BC.
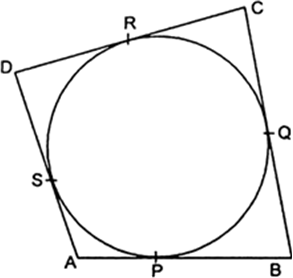
∴ AP = AS ...(i)
BP = BQ ...(ii)
CR = CQ ...(iii)
और DR = DS ...(iv)
समीकरण (i), (ii), (iii), व (iv) को जोड़ने पर
AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
अत: AB + CD = BC + DA.
सलंग्न आकृति में XY तथा X'Y', O केंद्र वाले किसी वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिंदु C पर स्पर्श रेखा AB, XY को A तथा X'Y' को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि  है।
है।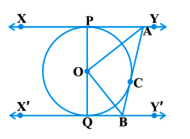
 प्राप्त होता है।
प्राप्त होता है। सिद्ध करना है:

रचना - O और C को मिलाइए। इसी प्रकार स्पर्श रेखाओं XY और X'Y' के स्पर्श बिंदु P और Q को O से मिलाएँ।
प्रमाण: क्योंकि XY स्पर्श रेखा है और OP एक त्रिज्या है।
∴
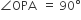 ...(i)
...(i)इसी प्रकार, AB स्पर्श रेखा है और OC एक त्रिज्या है।
∴
 ...(ii)
...(ii)अब समकोण
 और समकोण
और समकोण  में,
में,AP = PC (बाह्य बिंदु से एक ही वृत्त की स्पर्श रेखाएँ)
 (प्रत्येक
(प्रत्येक  )
)OA = OA (उभयनिष्ठ)
अत:
 (समकोण-कर्ण भुजा सर्वांगसम नियम से)
(समकोण-कर्ण भुजा सर्वांगसम नियम से)
 ...(iii)
...(iii)इसी प्रकार
 ...(iv)
...(iv)समीकरण (iii) व (iv) से,
 [∵ POQ एक सरल रेखा है]
[∵ POQ एक सरल रेखा है]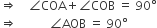
सिद्ध कीजिए कि किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है।
सिद्ध करना है:

रचना: A व B को वृत्त के केंद्र O से मिलाओ।
प्रमाण: क्योंकि PA स्पर्श रेखा है और त्रिज्या है।

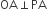

 ...(i)
...(i)इसी प्रकार,
 ...(ii)
...(ii)चतुर्भुज PAOB में,



अत: एक वृत्त पर एक बाह्य बिंदु से खींची गई स्पर्श रेखाओं के बीच कोण का स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपर्क होता है।
सिद्ध कीजिए कि किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।
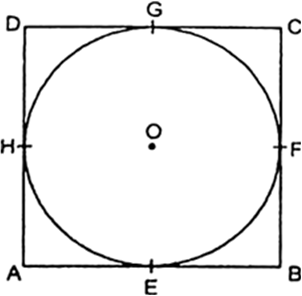
हम जानते हैं कि किसी वृत्त पर बाह्य बिंदु से खींची गई स्पर्श रेखाएँ समान होती है।
∴ AE = AH ...(i) [बिंदु Aसे वृत्त पर स्पर्श रेखाएँ]
BE = BF ....(ii) [बिंदु B से वृत्त पर स्पर्श रेखाएँ]
CG = CF ...(iii) [बिंदु C से वृत्त पर स्पर्श रेखाएँ]
और DG = DH ....(iv) [बिंदु D से वृत्त पर स्पर्श रेखाएँ]
समीकरण (i), (ii), (iii) व (iv) को जोड़ने पर,
AE + BE + GC + DG = AH + BF + CF + DH
⇒ (AE + BE) + (GC + DG)
= (AH + DH) + (BF + CF)
⇒ AB + CD = AD + BC
⇒ 2 AB = 2BC
या AB = BC
इसलिए समानांतर चतुर्भुज ABCD में AB = BC = CD = AD
अत: ABCD एक समचतुर्भुज है।
Sponsor Area
4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिंदु D द्वारा BC विभाजित है) की लंबाइयाँ क्रमश: 8cm और 6cm हैं। भुजाएँ AB और AC ज्ञात कीजिए।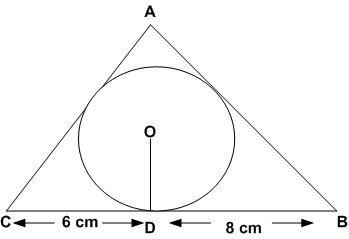
माना,  का अंत: केंद्र O इस प्रकार है कि-
का अंत: केंद्र O इस प्रकार है कि-
OD = OE = OF = 4 cm
BD = BE = 8 cm (बाह्य बिंदु B से स्पर्श रेखाएँ)
CD = CF = 6cm (बाह्य बिंदु C से स्पर्श रेखाएँ)
माना AF = AE = x cm (बाह्य बिंदु A से स्पर्श रेखाएँ)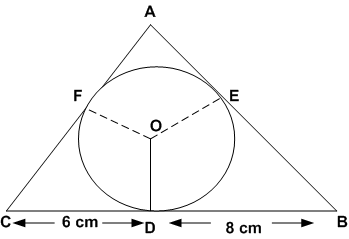
अब
AB = AE + BE = (x+8) cm
AC = AF + CF = (x+6) cm
BC = CD + BD = 6 + 8 = 14 cm
अब  में,
में,
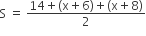
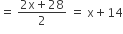
त्रिभुज ABC का क्षेत्रफल
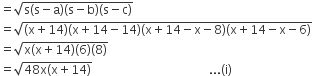
परन्तु,  का क्षेत्रफल =
का क्षेत्रफल =  का क्षेत्रफल,
का क्षेत्रफल, 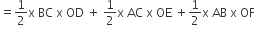
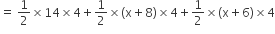
= 28 + 2 (x + 8) + 2 (x + 6)
= 28 + 2x + 16 + 2x + 12
= 4x + 56 ...(ii)
समीकरण (i) व (ii) की तुलना से'
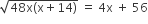
दोनों ओर का वर्ग करने पर,
48x (x + 14) = (4x + 56 )2 ![]() 48x (x + 14) = (4 (x + 14)]2
48x (x + 14) = (4 (x + 14)]2 ![]() 48x (x + 14) = 16 (x + 14)]2
48x (x + 14) = 16 (x + 14)]2 ![]() 3x (x + 14) = (x + 14)2
3x (x + 14) = (x + 14)2 ![]() 3x (x + 14) - (x + 14)2 = 0
3x (x + 14) - (x + 14)2 = 0![]() (x + 14) [3x - (x + 14)] = 0
(x + 14) [3x - (x + 14)] = 0![]() 3x - x - 14 = 0
3x - x - 14 = 0![]() 2x - 14 = 0
2x - 14 = 0![]() 2x = 14
2x = 14![]() x = 7
x = 7
अत: AB = x + 8 = 7 + 8 = 15 cm
AC = x + 6 = 7 + 6 = 13 cm
सिद्ध कीजिए कि वृत्त के परिगत बनी चतुर्भुज की आमने-सामने की भुजाएँ केंद्र पर संपूरक कोण अंतरित करती हैं।
दिया है: एक वृत्त जिसका केंद्र O है जोकि एक चतुर्भुज ABCD की भुजाओं AB, BC, CD और को क्रमश: बिंदुओं P, Q, R और S पर स्पर्श करता है।
सिद्ध करना है: 

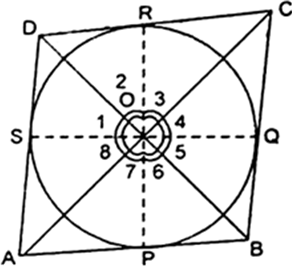
रचना: OP, OQ, OR तथा OS को मिलाइए।
प्रमाण: हम जानते हैं की बाह्य बिंदु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाएँ वृत्त के केंद्र पर समान कोण अंतरित करती हैं।
∴ 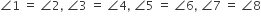
हम जानते हैं कि बिंदु O पर बने सभी कोणों का योग 360° होता है। 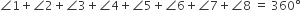
या 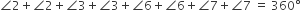

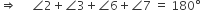
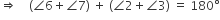

इसी प्रकार,
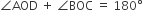
एक वृत्त खींचिए और दो एक दी गई रेखा के समांतर दो ऐसी रेखाएँ खींचिए की उनमें से एक स्पर्श रेखा हो तथा दूसरी छेदक रेखा हो।
दी गई रेखा l के समांतर दो रेखाएँ m और n खींचिए। अब रेखाओं l, m और n से एक लंब xy खींचिए। रेखाखंड xy पर एक बिंदु O तथा रेखा m पर बिंदु P लीजिए। O केंद्र तथा OP को त्रिज्या लेकर वृत्त खींचिए जो n को Q तथा R पर प्रतिच्छेद करे। इस प्रकार m स्पर्श रेखा तथा n छेदक रेखा होगी।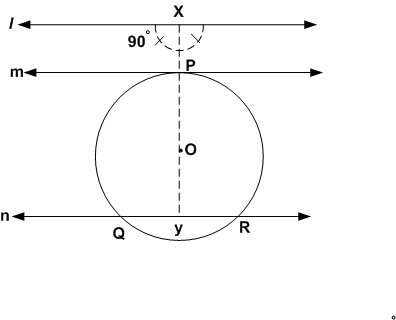
आकृति 7 में, दो चाप PAQ दर्शाई गई हैं। चाप PAQ, O केन्द्र वाले वृत्त का भाग है, जिसकी त्रिज्या OP है तथा चाप PBQ, PQ को व्यास मान कर बनाया गया अर्धवृत्त है जिसका केंद्र M है। यदि OP = 10 सेमी तथा PQ = 10 सेमी तो दर्शाइए कि रेखांकित भाग का क्षेत्रफल  है।
है।
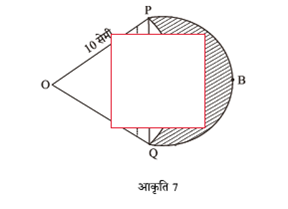
हम जानते हैं कि,
OP = OQ = 10 cm
PQ = OQ = PQ = 10 cm
3 सेमी तथा 5 सेमी त्रिज्या वाले दो संकेन्द्रीय वृत्त खींचिए। बड़े वृत्त के किसी बिंदु से छोटे वृत्त पर एक स्पर्श रेखा खींचिए। उसकी लम्बाई भी मापिए।
हम जानते हैं, OD = 3 cm और OP = 5 cm

PA और PB आवश्यक स्पर्शरेखा हैं।
माप से PA = PB = 4 cm
सिध्द कीजिए कि एक वृत्त के व्यास के अंत बिंदुओं पर खींची गई स्पर्श रेखाएँ परस्पर समान्तर होती हैं।
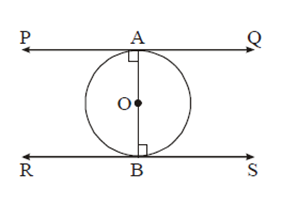
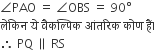
स्पर्श रेखाएँ परस्पर समान्तर होती हैं।
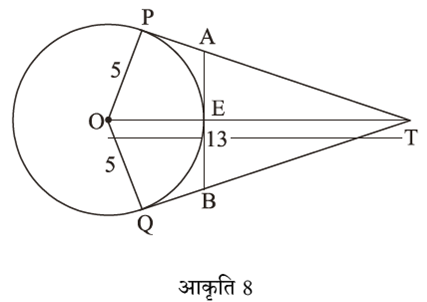
O केंद्र वाले वृत्त पर एक बाह्म बिंदु T से दो स्पर्श रेखाएँ TP तथा TQ खींची गई हैं। सिध्द कीजिए कि 

दिया है : TP और TQ एक सर्कल की दो स्पर्शरेखाएँ हैं। केंद्र O और P और Q संपर्क के बिंदु हैं।
सिद्ध करना : ∠PTQ=2∠OPQ
मान लीजिए, ∠PTQ=θ
अब प्रमेय के अनुसार, "एक बाहरी बिंदु से एक वृत्त में खींची गई स्पर्शरेखा की लंबाई बराबर होती है"
इसलिए, TPQ एक आइसोकेलस त्रिकोण है।
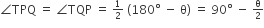
इसके अलावा प्रमेय के अनुसार "किसी भी बिंदु के स्पर्शरेन्ट त्रिज्या के संपर्क के बिंदु से लंबवत हैं" ∠OPT = 90 °,
अतः,
∠OPQ=∠OPT−∠TPQ
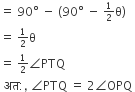
सिद्ध कीजिए कि एक बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाई बराबर होती है
O में केंद्रित एक वृत्त खींचे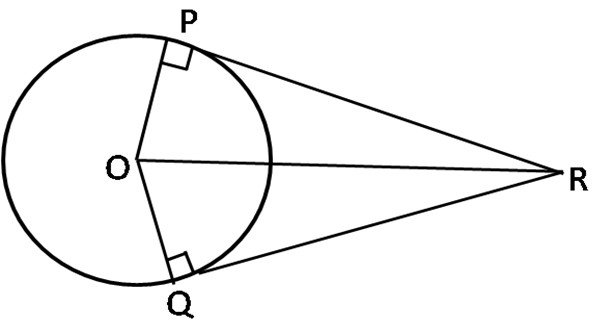
ΔOPR और ΔOQR में,
OP=OQ (एक ही वृत्त की त्रिज्या है)
∠OPR =∠OQR (PR और QR बाह्य बिंदु R से वृत्त पर खींची गई स्पर्श रेखा)
OR=OR (सामान्य पक्ष)
∆OPR ≅ ∆OQR (By R.H.S)∴ PR = QR (C.P.C.T)
इस प्रकार,एक बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाई बराबर होती है
Mock Test Series
Sponsor Area
Sponsor Area