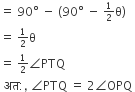O केंद्र वाले वृत्त पर एक बाह्म बिंदु T से दो स्पर्श रेखाएँ TP तथा TQ खींची गई हैं। सिध्द कीजिए कि $angle space PTQ space equals space 2 angle space OPQ$

Solution

दिया है : TP और TQ एक सर्कल की दो स्पर्शरेखाएँ हैं। केंद्र O और P और Q संपर्क के बिंदु हैं।
सिद्ध करना : ∠PTQ=2∠OPQ
मान लीजिए, ∠PTQ=θ
अब प्रमेय के अनुसार, "एक बाहरी बिंदु से एक वृत्त में खींची गई स्पर्शरेखा की लंबाई बराबर होती है"
इसलिए, TPQ एक आइसोकेलस त्रिकोण है।

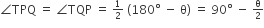
angle TPQ space equals space angle TQP space equals space begin inline style 1 half end style space left parenthesis 180 degree space minus space straight theta right parenthesis space equals space 90 degree space minus space begin inline style straight theta over 2 end style

इसके अलावा प्रमेय के अनुसार "किसी भी बिंदु के स्पर्शरेन्ट त्रिज्या के संपर्क के बिंदु से लंबवत हैं" ∠OPT = 90 °,
अतः,
∠OPQ=∠OPT−∠TPQ

equals space 90 degree space minus space left parenthesis 90 degree space minus space begin inline style 1 half end style straight theta right parenthesis equals space begin inline style 1 half end style straight theta equals space begin inline style 1 half end style angle PTQ space अत colon comma space angle PTQ space equals space 2 angle OPQ space

Some More Questions From वृत्त Chapter

For Daily Free Study Material Join wiredfaculty

वृत्त

O केंद्र वाले वृत्त पर एक बाह्म बिंदु T से दो स्पर्श रेखाएँ TP तथा TQ खींची गई हैं। सिध्द कीजिए कि $angle space PTQ space equals space 2 angle space OPQ$

Some More Questions From वृत्त Chapter

वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को ............. कहते हैं।

एक वृत्त के परिगत एक चतुर्भुज खींचा गया है (देखिए सलंग्न आकृति)। सिद्ध कीजिए:
AB + CD = AD + BC.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

वृत्त

O केंद्र वाले वृत्त पर एक बाह्म बिंदु T से दो स्पर्श रेखाएँ TP तथा TQ खींची गई हैं। सिध्द कीजिए कि

Some More Questions From वृत्त Chapter

वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को ............. कहते हैं।

एक वृत्त के परिगत एक चतुर्भुज खींचा गया है (देखिए सलंग्न आकृति)। सिद्ध कीजिए:AB + CD = AD + BC.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

O केंद्र वाले वृत्त पर एक बाह्म बिंदु T से दो स्पर्श रेखाएँ TP तथा TQ खींची गई हैं। सिध्द कीजिए कि $angle space PTQ space equals space 2 angle space OPQ$

एक वृत्त के परिगत एक चतुर्भुज खींचा गया है (देखिए सलंग्न आकृति)। सिद्ध कीजिए:
AB + CD = AD + BC.