4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिंदु D द्वारा BC विभाजित है) की लंबाइयाँ क्रमश: 8cm और 6cm हैं। भुजाएँ AB और AC ज्ञात कीजिए।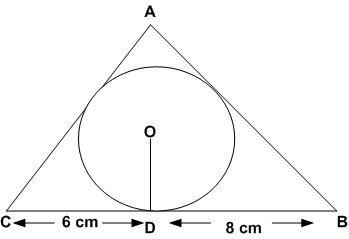

  

माना,  का अंत: केंद्र O इस प्रकार है कि-
                 OD = OE = OF = 4 cm
                      BD = BE = 8 cm        (बाह्य बिंदु B से स्पर्श रेखाएँ)
                      CD = CF = 6cm         (बाह्य बिंदु C से स्पर्श रेखाएँ)
माना          AF = AE = x cm               (बाह्य बिंदु A से स्पर्श रेखाएँ)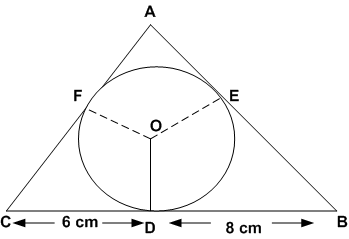

अब 
                   AB = AE + BE = (x+8) cm
                   AC = AF + CF = (x+6) cm
                   BC = CD + BD = 6 + 8 = 14 cm
अब  में,
                     
                         
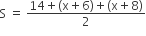
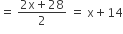
त्रिभुज ABC का क्षेत्रफल 

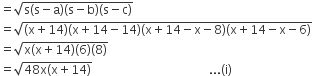
परन्तु,  का क्षेत्रफल  =  का क्षेत्रफल,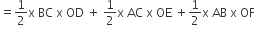 


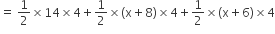
= 28 + 2 (x + 8) + 2 (x + 6)
= 28 + 2x + 16 + 2x + 12
= 4x + 56                                                ...(ii)
समीकरण (i) व (ii) की तुलना से'
        
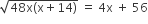
दोनों ओर का वर्ग करने पर, 
      48x (x + 14) = (4x + 56 )²    
  48x (x + 14) = (4 (x + 14)]² 
  48x (x + 14) = 16 (x + 14)]² 
   3x (x + 14) = (x + 14)² 
  3x (x + 14) - (x + 14)²  = 0
 (x + 14) [3x - (x + 14)] = 0
   3x - x - 14 = 0
   2x - 14 = 0
          2x = 14
            x = 7
अत:         AB = x + 8 = 7 + 8  = 15 cm
               AC = x + 6 = 7 + 6  = 13 cm