Question
सिद्ध कीजिए कि किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।
Solution
माना ABCD एक समांतर चतुर्भुज हैं जिसकी चारों भुजाएँ एक वृत्त को जिसका केंद्र O हैं EFGH बिंदुओं पर स्पर्श करती हैं।
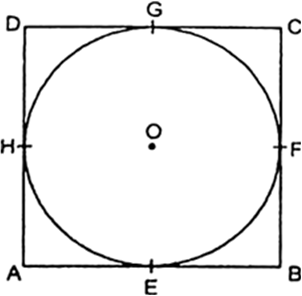
हम जानते हैं कि किसी वृत्त पर बाह्य बिंदु से खींची गई स्पर्श रेखाएँ समान होती है।
∴ AE = AH ...(i) [बिंदु Aसे वृत्त पर स्पर्श रेखाएँ]
BE = BF ....(ii) [बिंदु B से वृत्त पर स्पर्श रेखाएँ]
CG = CF ...(iii) [बिंदु C से वृत्त पर स्पर्श रेखाएँ]
और DG = DH ....(iv) [बिंदु D से वृत्त पर स्पर्श रेखाएँ]
समीकरण (i), (ii), (iii) व (iv) को जोड़ने पर,
AE + BE + GC + DG = AH + BF + CF + DH
⇒ (AE + BE) + (GC + DG)
= (AH + DH) + (BF + CF)
⇒ AB + CD = AD + BC
⇒ 2 AB = 2BC
या AB = BC
इसलिए समानांतर चतुर्भुज ABCD में AB = BC = CD = AD
अत: ABCD एक समचतुर्भुज है।
